\(y=ax^2\) のグラフ
\(2\) 乗に比例 \(y=ax^2\) のグラフがどのようなものか、学習していきましょう。
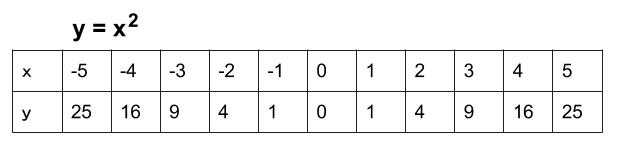
\(y=x^2\) のグラフ
式 \(y=x^2\) を満たす点をとっていき、その無限個の点の集合がグラフとなります。
もちろん、格子点以外の点、例えば\((0.5,0.25)\) などの点も通っています。
少し調べればわかりますが、 \(y=x^2\) を満たす点は一直線上には並びません。
グラフは曲線になるため、正確なグラフをかくにはたくさんの点を取って結ばないといけません。
しかし無限個の点はもちろん、\(100\) 個の点をとることでさえ現実的ではありません。
グラフの概形が下図のような曲線になることは、覚えてしまいましょう。
\(y=x^2\) のグラフ
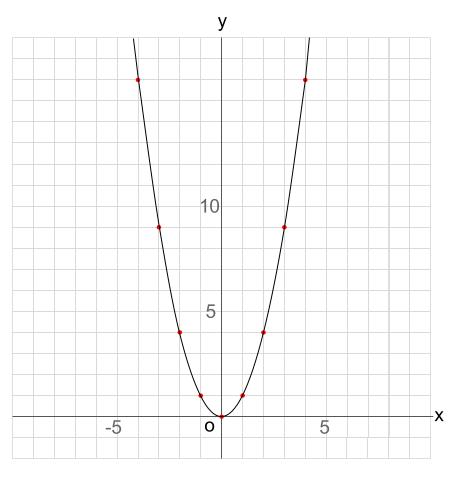
\(x\) が原点から遠ざかると、急激に上昇していくグラフになります。
今回の範囲では \((5,25)\) の点までかくことはできませんでした。
関数 \(y=x^2\) のグラフは、原点を通り \(y\) 軸について対称のグラフになります。
この曲線を放物線といいます。
\(y\) の値が負になることはありません。
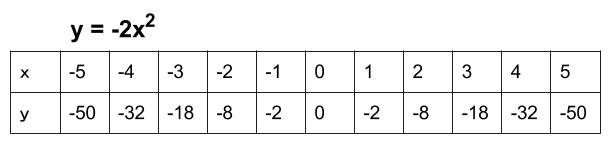
\(y=-2x^2\) のグラフ
同様に、\(y=-2x^2\) のグラフを書いてみましょう。
比例定数が負の数 \((-2)\) のグラフです。
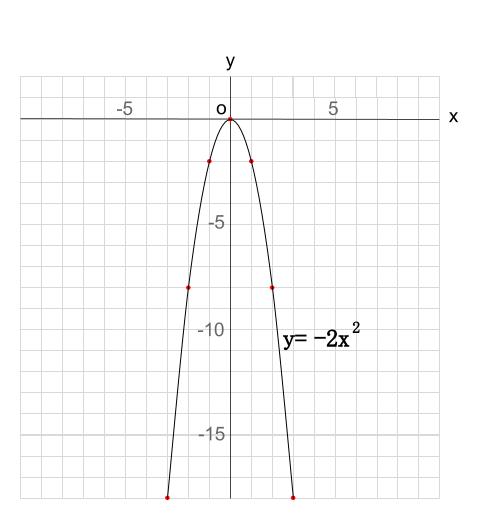
今回の範囲では \((3,-18)\) の点までしかかくことはできませんでした。
比例定数が負の数のとき、正のときのグラフと \(x\) 軸について対称になります。
\(y\) の値が正になることはありません。
グラフのかき方
さて、上で見た \(y=x^2\) のグラフを、実際に自分で書いてみましょう。
\(2\) 乗に比例のグラフは曲線なので、完璧に正確なグラフを書くことはできません。
通るべき格子点を通り、あとはできるだけなめらかな曲線で結びます。
曲線部分は、あまり正確さにこだわる必要はありません。
放物線は、こんな曲線になる!
という知識をもとに、再現するのです。
スポンサーリンク
