平行線と線分の比の利用
平行線と線分の比を用いる問題を練習しましょう。
\(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。
例題1
次の図で、直線 \(L,M,N\) が平行のとき、\(x\) の値を求めなさい。
①
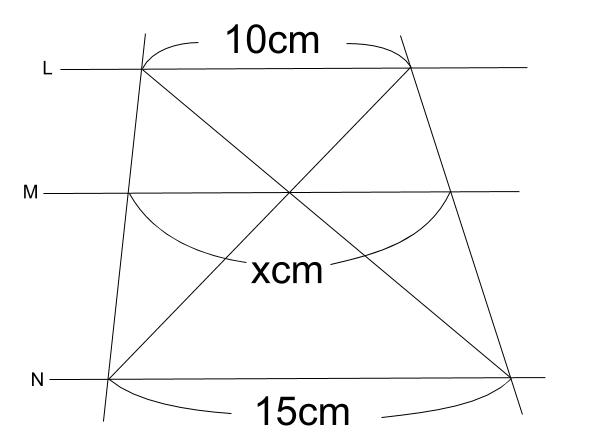
②
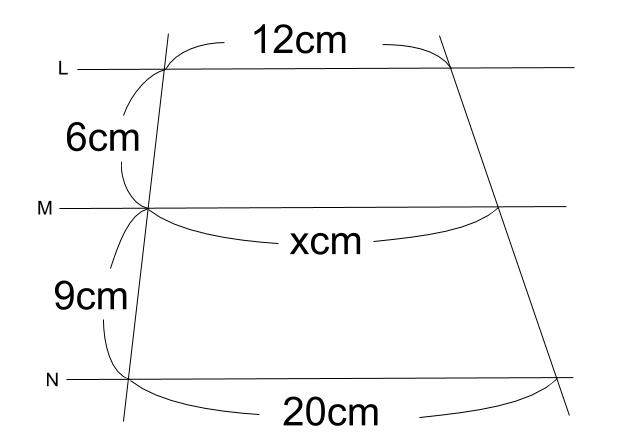
解説
①と②で似たような図です。
もちろんどちらも似たような解き方で解けます。
どちらも、「相似」や「平行線と線分の比」の利用で解きます。
ただし・・・
①をいわゆる「公式」で習ったことがある人が、
その「公式」を何も考えないで②に適用すると
大間違いとなってしまいます。
「公式」とは何なのか、これに関しても後で説明をしますが、
「公式」を用いない解法をおすすめしたいと思います。
①の解説
まず、平行線があるので、
最重要図形の1つである「砂時計型」に気づけるようになりましょう。
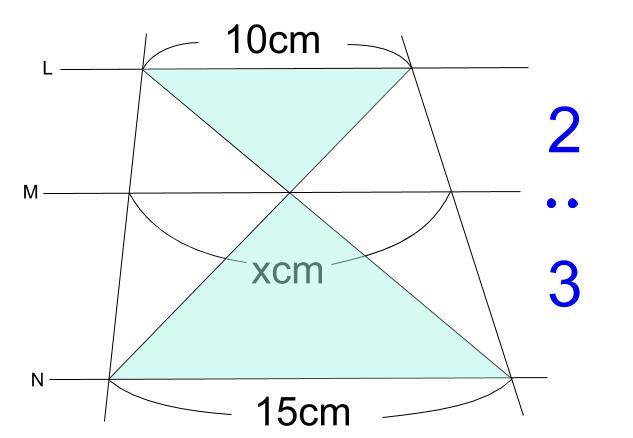
相似比は、\(10:15=2:3\) です。
対応する線分の比は \(2:3\) なので
下の図の赤い線分の比が \(2:3\) です。
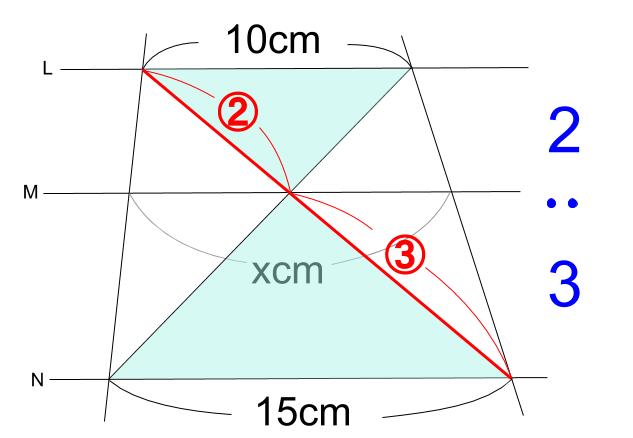
これは、下の図のピラミッド型の線分の比でもあります。
ピラミッド型の相似比は \(2:2+3=2:5\) とわかります。
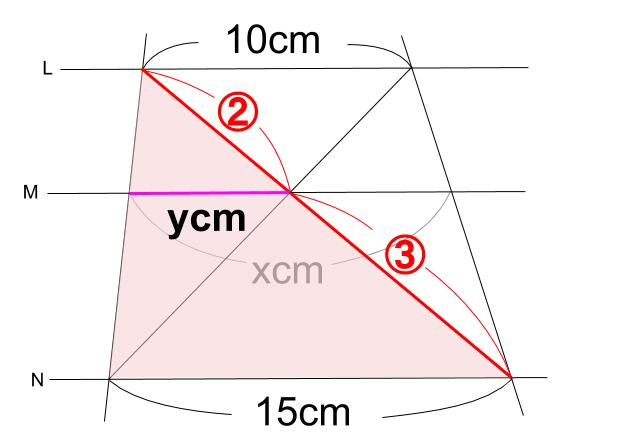
よって、ピンク色の線分の長さ \(ycm\) は
\(y=15×\displaystyle \frac{2}{5}=6(cm)\) と求まります。
まったく同じように、下図のピラミッド型から、
\(z=15×\displaystyle \frac{2}{5}=6(cm)\) と求まります。
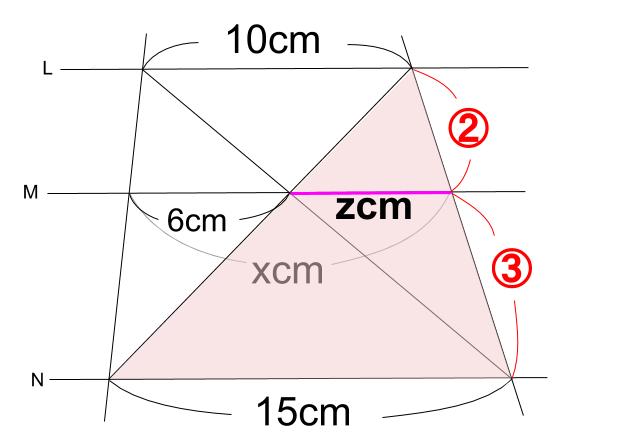
つまり、
\(x=y+z=6+6=12(cm)\)
と求まります。
公式による別解
先ほど書いた「公式」についてです。
この図に関してだけ成り立つ公式があります。
下の図で、直線 \(L,M,N\) が平行のとき
\(y=z=\displaystyle \frac{ab}{a+b}\)
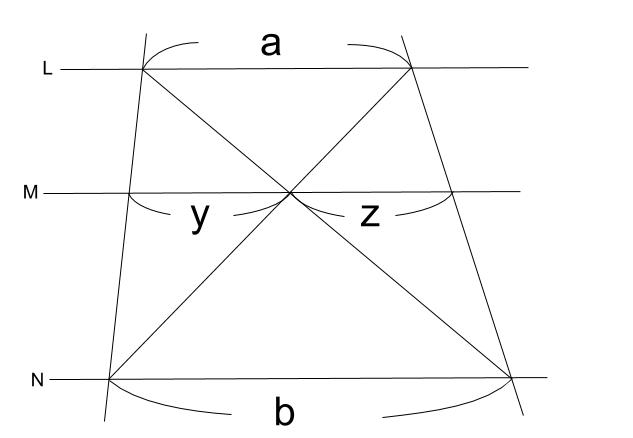
なぜ成立するのかは、上の解説の通りに解けば出てきます。
先の①をこの公式を用いて解くと、
\(x=\displaystyle \frac{10×15}{10+15}×2=12\)
と求まります。
先ほどの解説のように解くよりも、
公式一発で解ければ確かに速いです。
これは疑いようがありません。
ですので、この「公式」を覚えて使うことに関して、
絶対に「ダメだ」とは言い切れないものがあります。
しかし、
筆者はこの「公式」はあまりおススメしたいものではありません。
その最大の理由は、汎用性がないからです。
つまり、使える図形が上のようなときだけだからです。
台形の対角線の交点に、底辺と平行な線が引かれているときです。
これ以外で出題されると、この公式は使えません。
②では使えないのです。
ですので、「公式」を利用しない解法、
つまり相似や平行線の扱いに慣れるような学習を進めてください。
その上で、「公式」も併用したければすれば良いと思います。
「公式」しか使えないと、まったく手も足もでない問題があるということは知っておいてください。
②の解説
解説の前に、②を再掲しておきましょう。
次の図で、直線 \(L,M,N\) が平行のとき、\(x\) の値を求めなさい。

では解説です。
②のよくある間違いの確認
先ほども書いた通りですが、この図では先の「公式」は使えません。
この問題で非常によくある間違いは、
下図のように考えてしまうことです。
何が間違いなのか、わかりますか?

何が間違っているのか。
ずばり・・・
この図では、台形の対角線の交点は、直線 \(M\) 上にはありません。
正しくは下図のようになります。
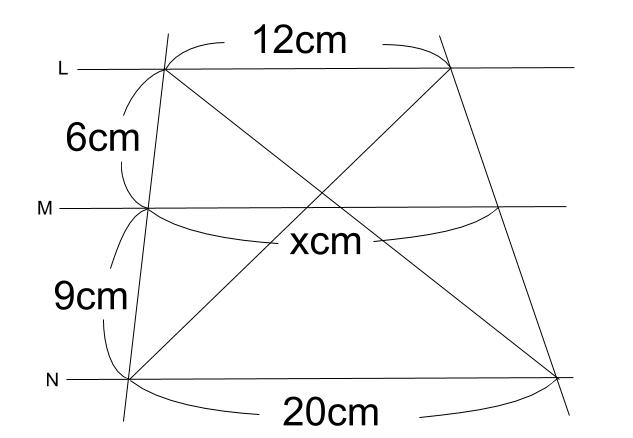
よって、先の「公式」は適用できませんし、
台形の対角線の交点が、直線 \(M\) 上にはあることを前提に
相似な図形を利用しても、正しい答えが得られません。
あらためて、②を解いていきましょう。
様々な解法がありますが、代表的な解法を紹介します。
②の解法
下図のように、赤い平行線を補助線として引きます。
すると、はじめの台形は、
ピラミッド型三角形と平行四辺形に分割されます。
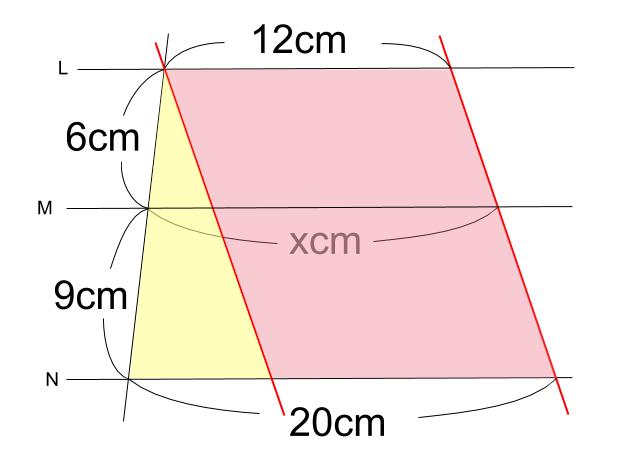
右の平行四辺形は、底辺が \(12cm\) なので
左のピラミッド型三角形の底辺が \(20-12=8cm\) とわかります。
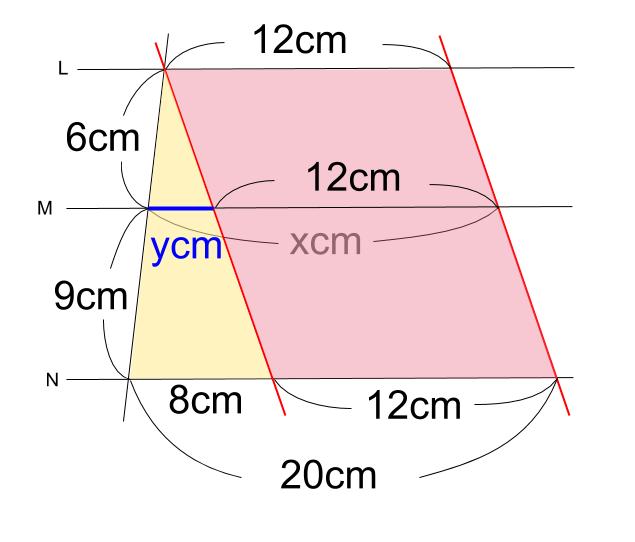
また、ピラミッド型三角形の相似比は \(6:6+9=2:5\) なので
青い長さ \(ycm\) は
\(y=8×\displaystyle \frac{2}{5}=3.2(cm)\)
よって、求める長さ \(x\) は
\(x=y+12=15.2\)
と求まります。
別解
台形の対角線のうち、\(1\) 本だけを引いて、
\(2\) つのピラミッド型を利用しても求まります。
挑戦してみましょう。
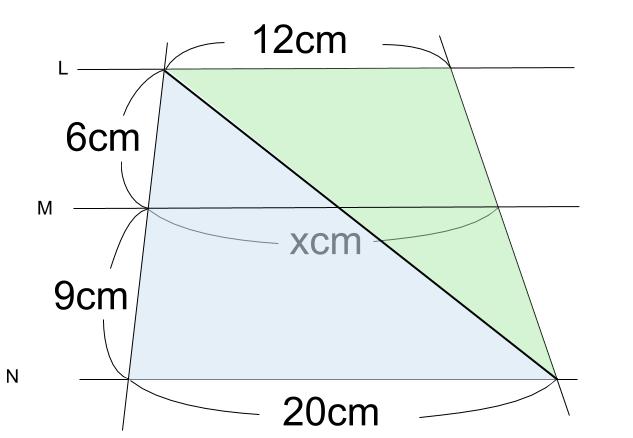
左、水色のピラミッドの内部の線分は \(20×\displaystyle \frac{2}{5}=8\)
右、緑色のピラミッドの内部の線分は \(12×\displaystyle \frac{3}{5}=7.2\)
より、\(x=8+7.2=15.2\)
と求まります。
