平行線と線分の比
下の図で、直線 \(L,M,N\) が平行ならば、線分の長さの比について以下のことが成りたつ。
\(AB:BC = DE:EF\)
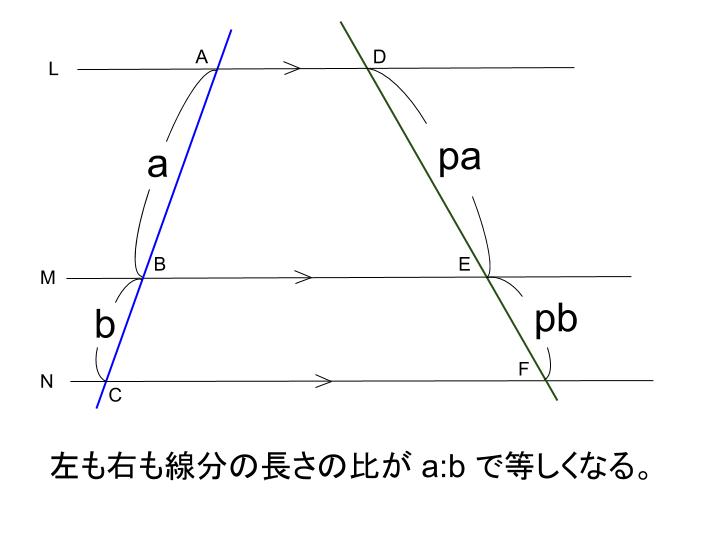
これはなぜ成り立つのか。
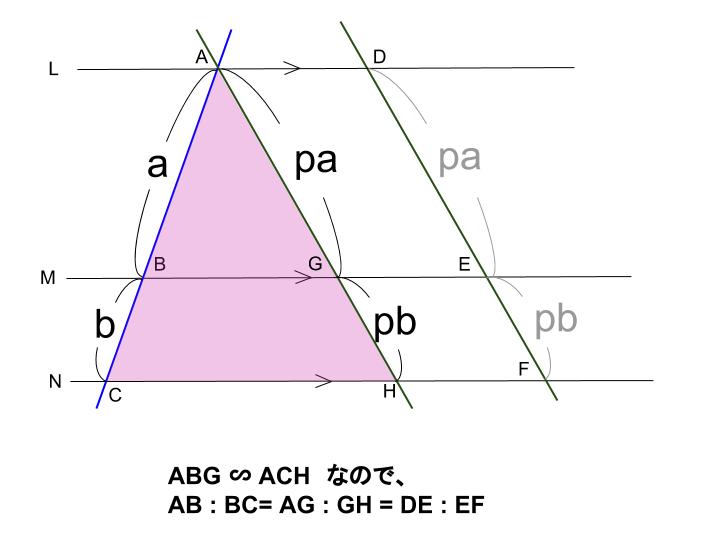
下の図のように、\(DF\) と平行な線分 \(AH\) を引けば、
ピラミッド型相似ができます。
これにより
\(AB:BC = AG:GH\) がわかります。
\(AG=DE\) かつ \(GH=EF\) なので
\(AB:BC = DE:EF\)
もわかります。
例題1
下の図で、直線 \(L,M,N\) が平行のとき、\(x\) の値を求めなさい。
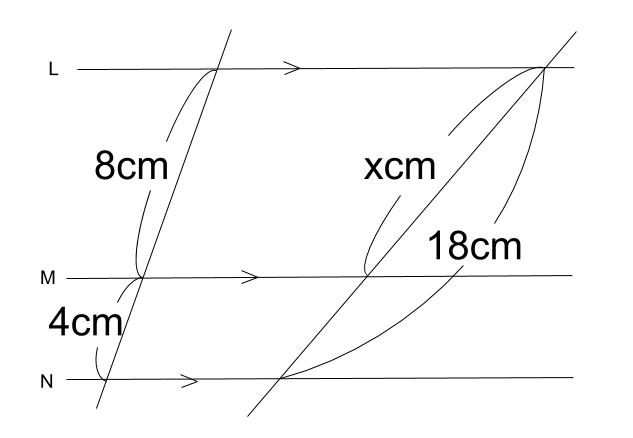
解説
平行線と線分の比の性質を覚えているかどうか、
それだけの問題ですよ。
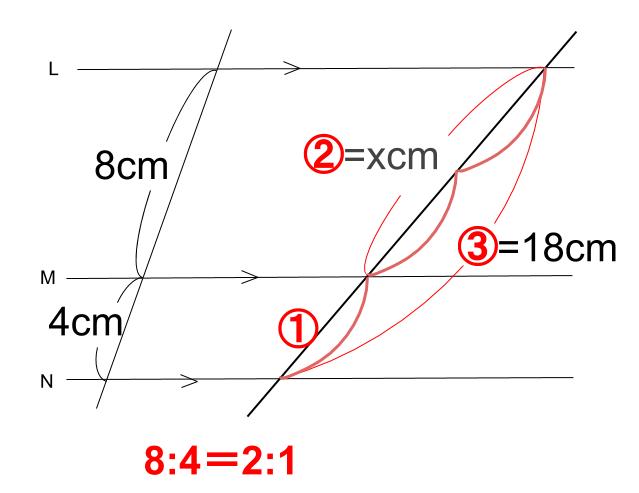
\(L~M\) 間と \(M~N\) 間との線分の比が
\(8:4=2:1\) になる。
これを利用すれば
\(x=18×\displaystyle \frac{2}{2+1}=12\)
より、
\(x\) の値は \(12\) です。
例題2
下の図で、直線 \(L,M,N\) が平行のとき、\(x\) の値を求めなさい。
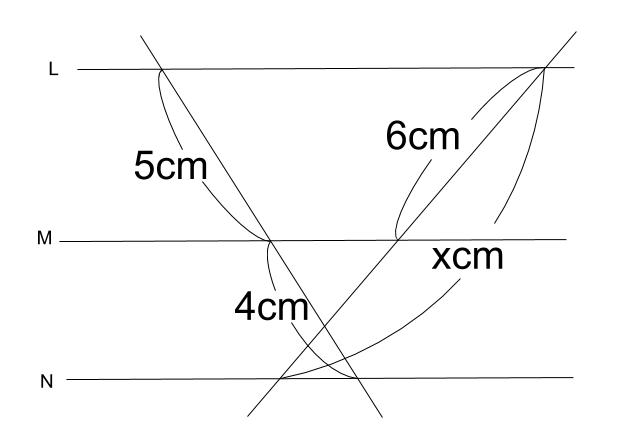
解説
直線が交わっていても、なんら関係ありません。
左の直線を、さらに左にずらしてみましょう。
ピラミッド型です。
※平行移動といいます。
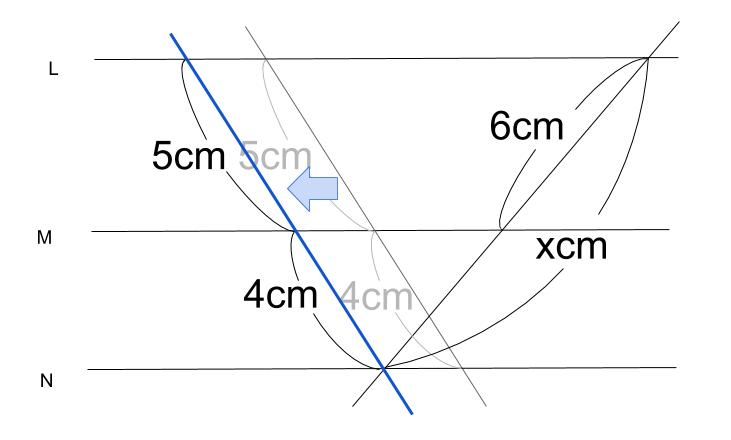
結局、平行線と線分の比の性質を使うだけです。
直線が交わっていても、なんら関係ないことがわかりましたね。
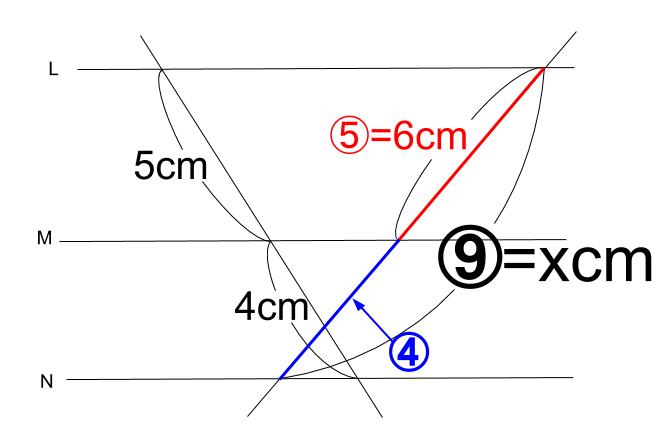
よって、
\(x=6×\displaystyle \frac{5+4}{5}=10.8\)
より、
\(x\) の値は \(10.8\) です。
