例題10
下の図の角 \(x\) の大きさを求めなさい。
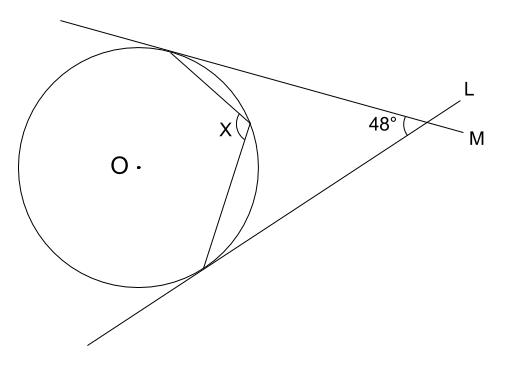
ただし、直線 \(L\) と直線 \(M\) は円 \(O\) の接線である。
解説
円と接線の性質を覚えていますか?
下図のように、円の中心と接点を結ぶ線と、接線は垂直になります。
重要暗記事項です。しっかり覚えましょう。
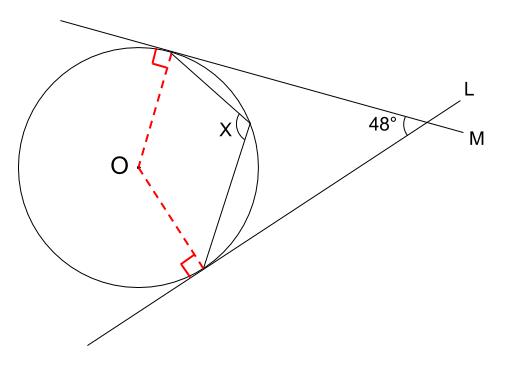
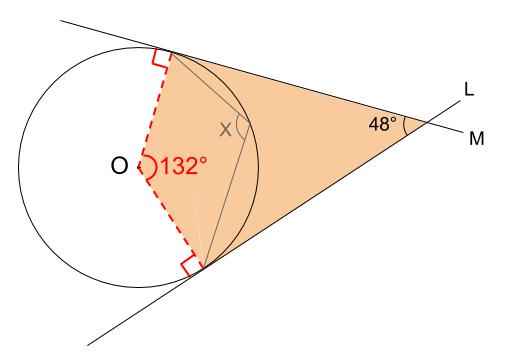
次に、下図のオレンジ色の四角形の内角より、左の赤い角の大きさが
\(360-(90+90+48)=132°\)
と求まります。
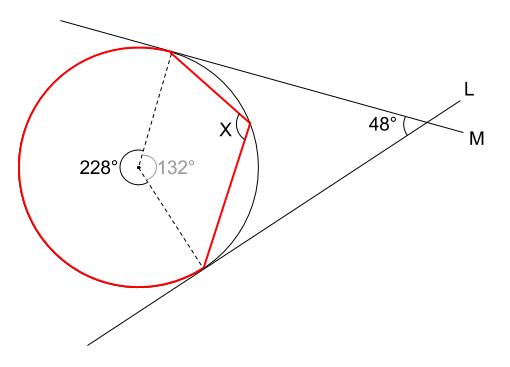
よって、下図の赤い弧の中心角と円周角に着目して、
\(x=228÷2=114°\)
と求まります。
例題11
下の図の角 \(x\) の大きさを求めなさい。
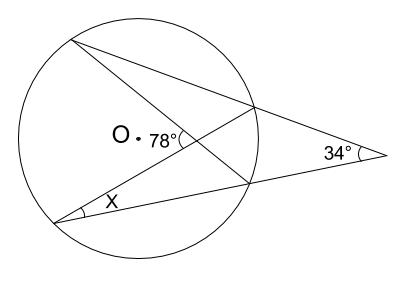
解説
下図の赤い弧の円周角の大きさが \(x\) です。
また青い弧の円周角の大きさを \(y\) とします。
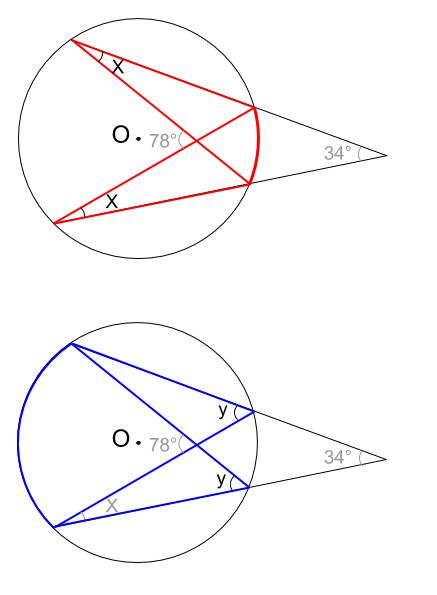
あとは、\(x\) と \(y\) の大きさについて方程式をたてることで求まります。
下図の水色の三角形の外角より、
\(y=x+34\)・・・①
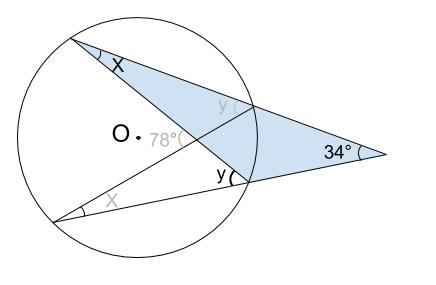
下図の黄色の三角形の外角より、
\(x+y=78\)・・・②
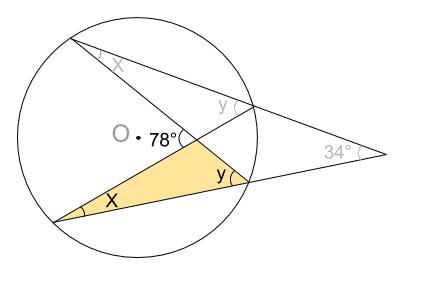
①と②を連立して解きます。
$\left\{ \begin{array}{@{}1} y=x+34\\ x+y=78 \end{array} \right. $
解
$\left\{ \begin{array}{@{}1} x=22\\ y=56 \end{array} \right. $
もちろん、聞かれている角の大きさは \(x=22°\) です。
