座標平面上の2点間の距離
座標平面上の \(2\) 点間の距離は、三平方の定理から求まります。
\(A(x_{1 },y_{1 })\),\(B(x_{2 },y_{2 })\) の間の距離は
\(AB=\sqrt{(x_{2 }-x_{1 })^2+(y_{2 }-y_{1 })^2}\)
これは公式を覚えるのではなくて、
三平方の定理を使えば求まる、と覚えます。
例題1
\(2\) 点 \(A(-4,1)\),\(B(2,-2 )\) の間の距離を求めなさい。
解答
座標平面と座標をラフにかきましょう。
ていねいにかく必要はありません。
長さも不正確でOKです。
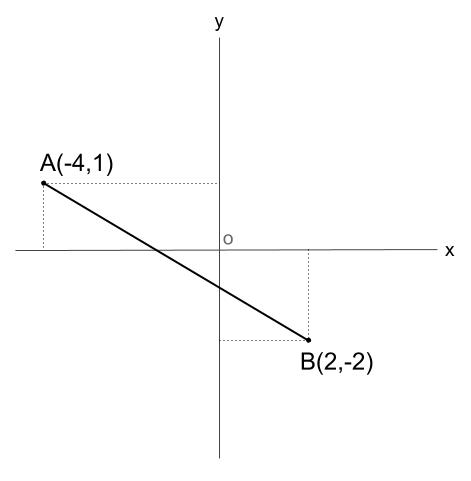
あとは、直角三角形をつくり、長さを入れます。
座標から長さがわかります。
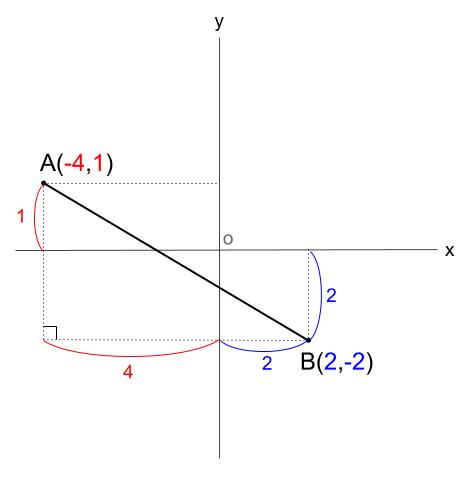
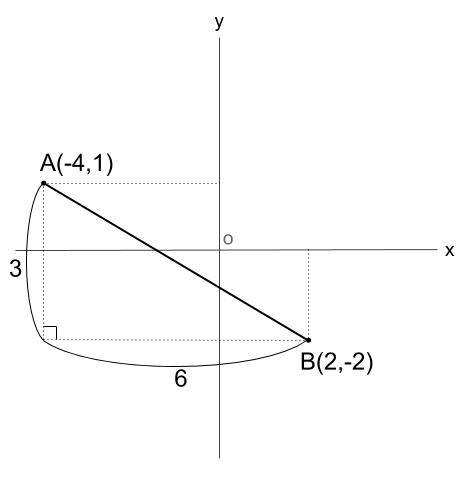
つまり、下の図のクリーム色の直角三角形に
三平方の定理を用います。
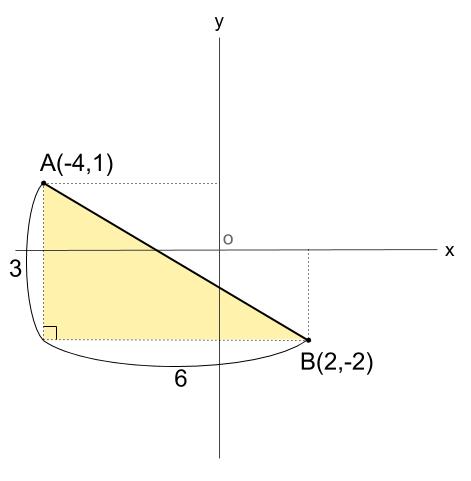
\(AB^2=3^2+6^2\)
\(AB^2=45\)
\(AB \gt 0\) なので
\(AB=\sqrt{45}\)
\(AB=3\sqrt{5}\)
