立体の表面の最短距離
立体の表面を結ぶ線分を考えるとき、展開図をかいて考えます。
重要な解法テクニックです。
例題1
下の図のように、直方体の頂点 \(B\) から、辺 \(CG\) を通って点 \(H\) まで
糸をまきつけた。糸の長さが最も短くなるとき、辺 \(CG\) 上の点 \(P\) を通った。
このとき、糸の長さを求めなさい。また、\(CP\) の長さを求めなさい。
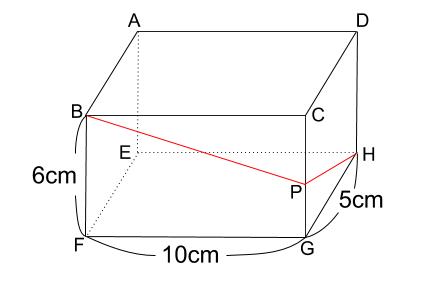
解答
直方体の展開図をかきます。
\(6\) 面すべてをかく必要はありません。
糸の通過している面のみをかきましょう。
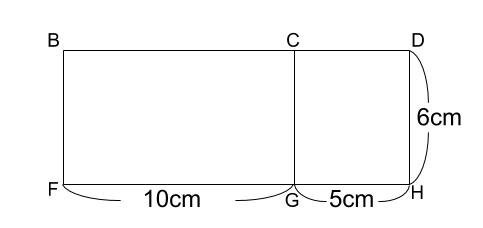
\(BH\) を結ぶ最短距離は、\(B\) と \(H\) を一直線に結んだ線分の距離です。
下図から明らかでしょう。
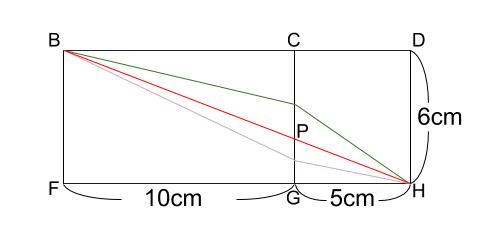
直角三角形 \(BFH\) の斜辺 \(BH\) の長さが、
最短の糸の長さです。
直角三角形 \(BFH\) に三平方の定理を用いて
\(BH^2=6^2+15^2\)
この計算は少し面倒ですね。
直角三角形 \(BFH\) と相似な三角形を利用できると
計算が楽です。
相似の利用を確認しておきましょう。
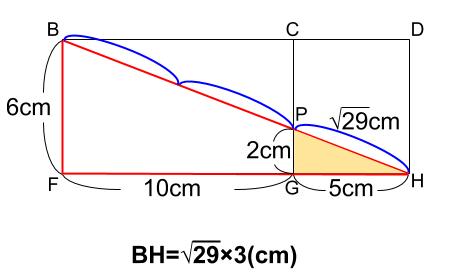
下の図のように、\(\triangle BFH \backsim \triangle PGH\)
いわゆるピラミッド型です。
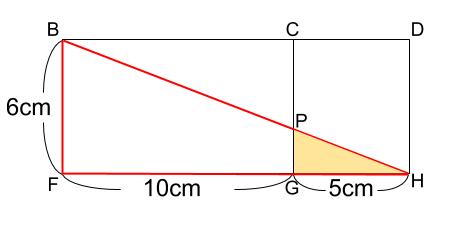
相似比は、\(FH:GH=15:5=3:1\) なので
対応する辺である、\(BF:PG=3:1\) です。
よって、\(PG=6×\displaystyle \frac{1}{3}=2cm\)
糸の長さより先に、 \(CP\) の長さが求まりましたね。
\(CP=6-2=4cm\) です。
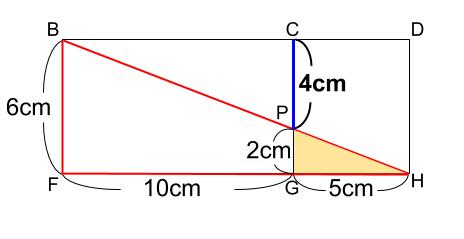
また、クリーム色の直角三角形 \(PGH\) に三平方の定理を用いると
\(PH^2=2^2+5^2\)
\(PH^2=29\)
\(PH \gt 0\) なので
\(PH=\sqrt{29}\)
\(\triangle BFH \backsim \triangle PGH\) の相似比は \(3:1\) なので、
対応する辺である、\(BH:PH=3:1\) です。
よって、
\(BH=\sqrt{29}×3\)
\(=3\sqrt{29}cm\)