三角定規型
暗記しておくべき直角三角形があります。
それは三角定規の形です。
三角定規は \(2\) 種類あります。
その \(2\) 種類は必ず暗記すべき特別な直角三角形です。
45° 45° 90°
まずはじめに直角二等辺三角形タイプです。
これは「正方形半分タイプ」という名前でも覚えておきましょう。
\(3\) 辺の比が、\(1:1:\sqrt{2}\) となることも暗記です。
もちろん暗記していなくとも三平方の定理で導けるのですが・・・
非常によく使うので暗記すべきです。
辺の比と角度、両方暗記しておきましょう。

30° 60° 90°
次に、「正三角形半分タイプ」です。
\(3\) 辺の比が、\(1:2:\sqrt{3}\) となることも暗記です。
もちろん暗記していなくとも三平方の定理で導けるのですが・・・
非常によく使うので暗記すべきです。
辺の比と角度、両方暗記しておきましょう。

これらの \(2\) つがなぜ大事なのかといえば、身もふたもなく
「非常によく出題されるから」です。
テストに。入試に。
もうめちゃくちゃ大事です。絶対暗記しなくてはいけません。
3辺が整数になるタイプ
三角定規型ほどの重要度はありませんが、次の直角三角形も覚えておいて損はありません。
\(3\) 辺の長さの比が、\(3:4:5\)
\(3\) 辺の長さの比が、\(5:12:13\)
となる直角三角形です。
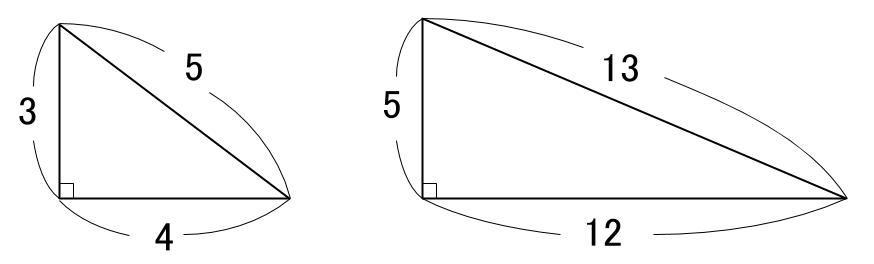
このように\(3\) 辺の長さの比が、すべて整数になるのはなかなか珍しいことなのです。
※\(3\) 辺の長さの比が、整数になる直角三角形をピタゴラス三角形といいます。他にも、\(7:24:25\) など、無数のピタゴラス三角形があります。
例題1
下の図の、\(x,y\) の値をそれぞれ求めなさい。
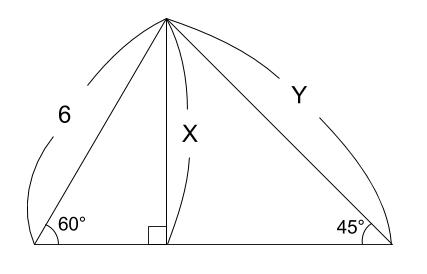
解答
左の直角三角形は、正三角形を半分にしたものです。
\(3\) 辺の比は暗記で、\(2:1:\sqrt{3}\) です。
よって、下の図のように長さが決まります。
\(x=3\sqrt{3}\) です。
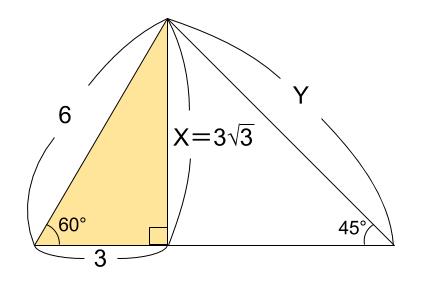
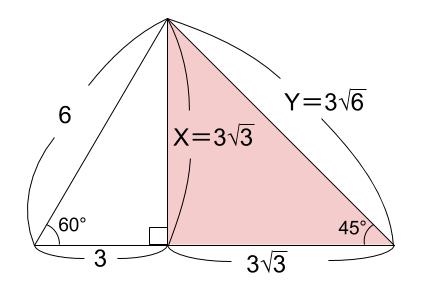
右の直角三角形は、正方形を半分にした直角二等辺三角形です。
\(3\) 辺の比は暗記で、\(1:1:\sqrt{2}\) です。
よって、下の図のように長さが決まります。
\(y=3\sqrt{6}\) です。
例題2
下の図の、\(x\) の値を求めなさい。
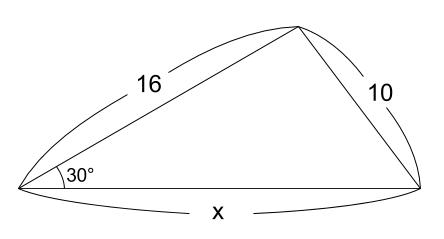
解答
\(30°\) とあるのですから、三角定規型を使うに決まっています。
下の図のように補助線を引きます。
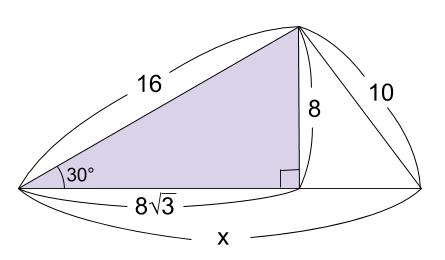
左の直角三角形が正三角形を半分にしたものです。
\(3\) 辺の比は暗記で、\(2:1:\sqrt{3}\) です。
次に、右の直角三角形に三平方の定理を使うと、
最後の \(1\) 辺の長さが求まります。
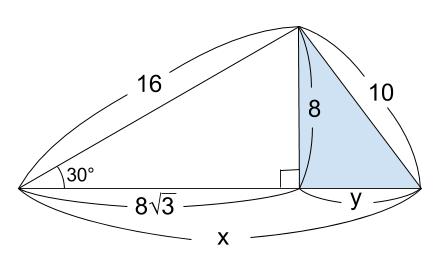
最後の \(1\) 辺の長さを \(y\) とすると
\(y^2+8^2=10^2\)
\(y^2+64=100\)
\(y^2=36\)
\(y=±\sqrt{36}\)
\(=±6\)
この問題では、もちろん \(y\) は正の値なので
\(y=6\)
よって、\(x=8\sqrt{3}+6\)
これで求まりました。
3:4:5タイプに気づいた?
例題2の \(y\) の値は、右の直角三角形が、
辺の比 \(3:4:5\) タイプであることに気づけば、
三平方の定理を用いずに求められます。
\(y:8:10=3:4:5\)
なので
\(y=6\)
