【中学数学】相似の重要形　ピラミッド型と砂時計型

相似な三角形の代表選手　ピラミッド　と　砂時計

平面図形パズルを解くカギとして、非常によく用いられる重要な要素があります。
それは、三角形の相似を利用した以下の図です。
※「パズルを解くカギとして、非常によく用いられる」と書きましたが、正しくは、
「問題を作成するさいによく利用される」です。
中学数学という非常に限られた範囲内での作問をするとき、どうしてもよく利用されるパターンが存在するのです。

砂時計型

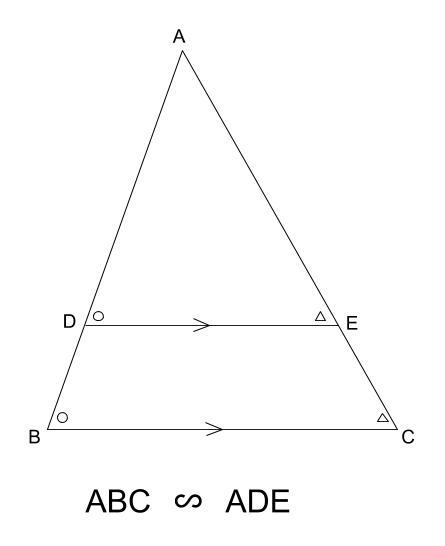
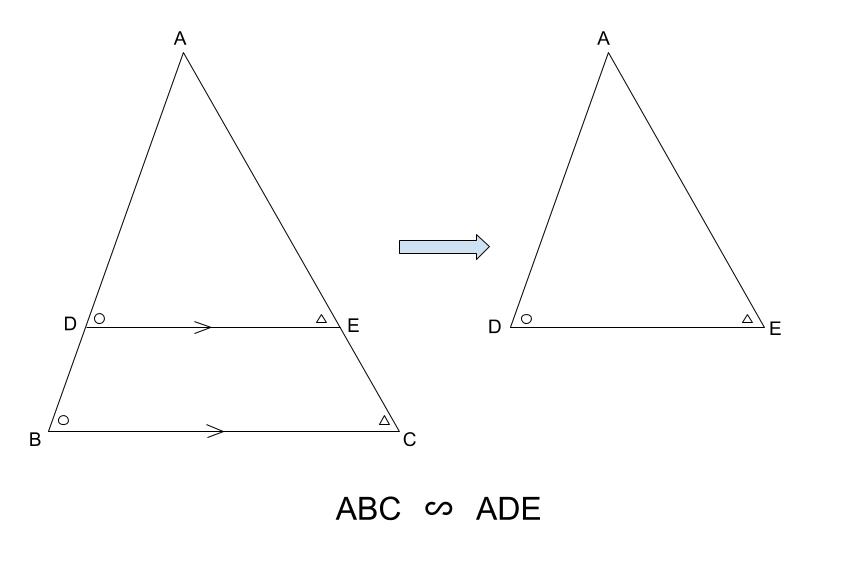
下の図の $\triangle ABC$ と $\triangle ADE$ で　$ED /\!/ BC$ のとき、
$\triangle ABC \backsim \triangle ADE$ が成り立ちます。
平行線の錯角が等しいために、$2$ つの三角形が相似であることがわかります。

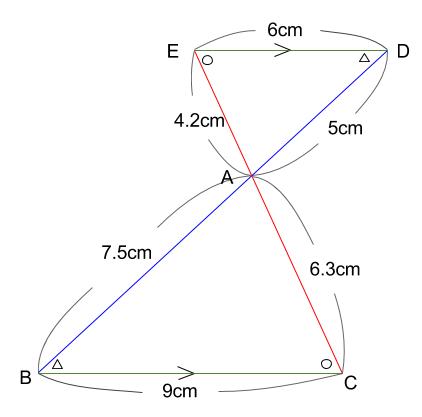
砂時計型という名称は塾業界での通称です。ちょうちょ型などと呼ばれることもあります。
正式名称はありません。当サイト内では「砂時計型」で通します。

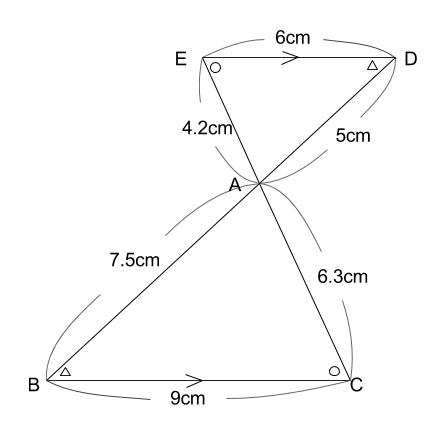
相似な $2$ つの三角形で、同じ色の辺同士が対応する辺です。
対応する辺の比が相似比です。

下図では相似比が $2:3$ になっています。
※$6:9=4.2:6.3=5:7.5=2:3$

ピラミッド型

下の図の $\triangle ABC$ と $\triangle ADE$ で　$DE /\!/ BC$ のとき、
$\triangle ABC \backsim \triangle ADE$ が成り立ちます。
平行線の同位角が等しいために、$2$ つの三角形が相似であることがわかります。

ピラミッド型という名称も塾業界での通称です。富士山型などと呼ばれることもあります。
正式名称はありません。当サイト内では「ピラミッド型」で通します。
ピラミッド型を扱うさい、$2$ つの三角形が重なっているために注意が必要です。
慣れるまでは、小さい三角形を横に書き写して、その図を見比べて解くことをお勧めします。

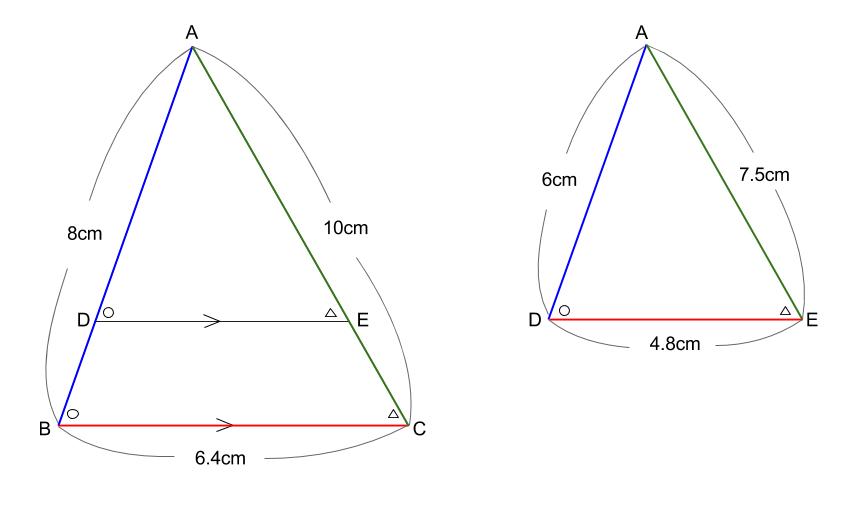
相似な $2$ つの三角形で、同じ色の辺同士が対応する辺です。
対応する辺の比が相似比です。

下図では相似比が $4:3$ になっています。
※$8:6=10:7.5=6.4:4.8=4:3$

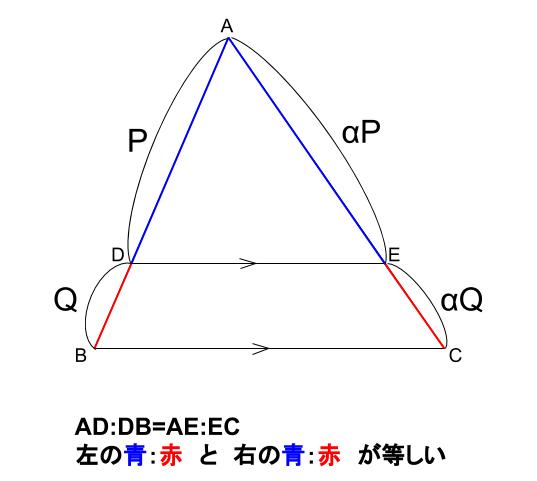
ピラミッド型の重要な線分の比

下の図において、
$AD:DB=AE:EC$
が成りたちます。

特別な名前もついていないのですが、
とても重要なのでしっかり覚えておきましょう。

例題１

下の図で、 $ED /\!/ BC$ のとき、 $x,y$ の値を求めなさい。

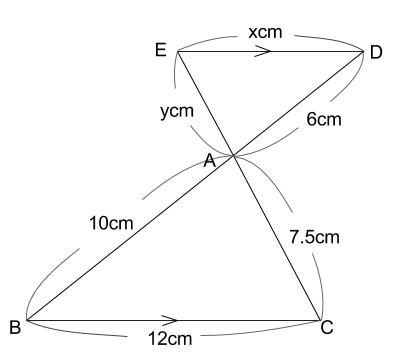
解説

平行線があれば、砂時計やピラミッドの出番です。
$\triangle ABC \backsim \triangle ADE$
ですね。
対応する線分、両方の長さがわかる箇所を探します。
$AB:AD=10:6=5:3$
相似比は $5:3$ です。
下図のように、上が $3$ で下が $5$ とわかるような比のかきかたは
公式ではありませんが、自分で解くためのメモとしては
とても便利です。

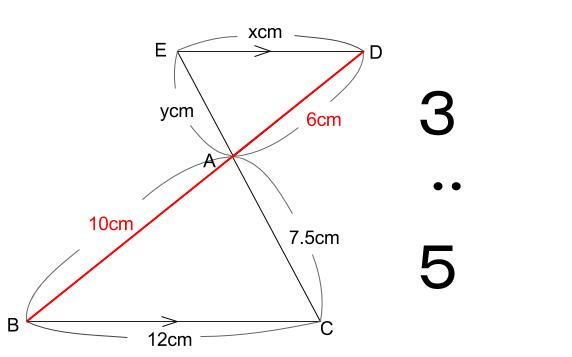
よって、他の対応する 辺の比も $5:3$ なので
$12:x=5:3$
$7.5:y=5:3$

が成りたちます。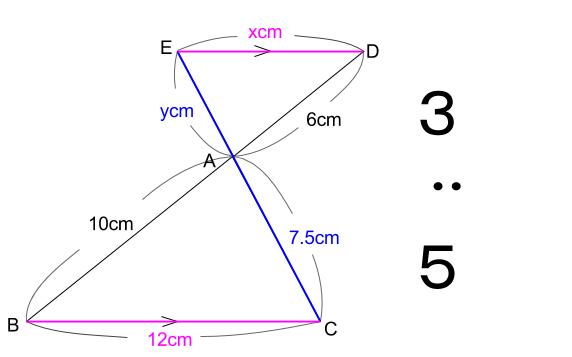

外項の積と内項の積は等しいので、
$12:x=5:3$
からは
$5x=12×3$
$x=7.2$
と求まります。

$7.5:y=5:3$
からは
$5y=7.5×3$
$y=4.5$
と求まります。

例題２

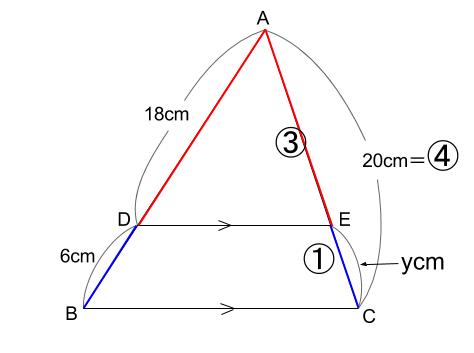
下の図で、 $BC /\!/ DE$ のとき、 $x,y$ の値を求めなさい。

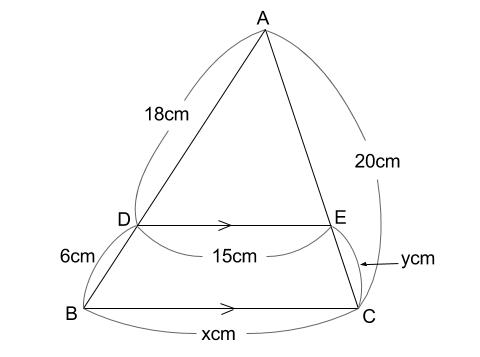
解説

平行線なので、ピラミッド形です。

慣れないうちは、小さい方を横にぬき出して解きましょう。
ミスが格段に減ります。
対応する辺を見て、相似比を求めます。
$AB:AD=4:3$
なので、相似比は $4:3$ です。

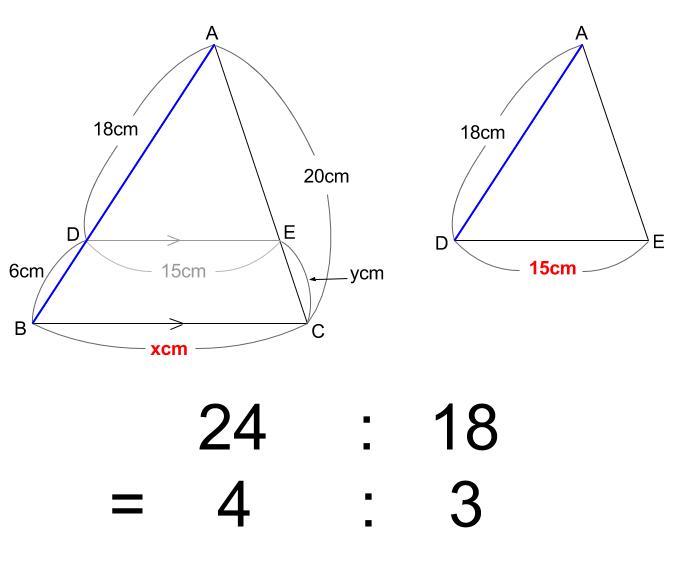
よって、$x:15=4:3$ なので
$x=20$
と求まります。

また、 $y$ ですが、
相似比を活用することで、$AE=15$ と求め、
$y=20-15=5$
と求めることもできますし、
下図の赤と青の線分の比が $18:6=3:1$
であることを用いて
$y=20×\displaystyle \frac{1}{3+1}=5$
と求めることも可能です。

• 次のページ 平行線と線分の比
• 前のページ 相似の証明・その２