【中学数学】2乗に比例の利用・動点・その２

例題１

$1$ 辺が $6cm$ の正方形 $ABCD$ とその辺上を動く$2$ 点 $P,Q$ がある。点$P$ は秒速$2cm$ で、点 $Ｂ$ を出発して $A$ を通り、点 $D$ まで動く。点 $Q$ は点 $P$ と同時に $B$ を出発し、秒速$1cm$ で点 $C$ まで動く。$2$ 点 $P,Q$ が同時に $B$ を出発してから $x$ 秒後の三角形 $BPQ$ の面積を $ycm^2$ とする。次の問いに答えなさい。

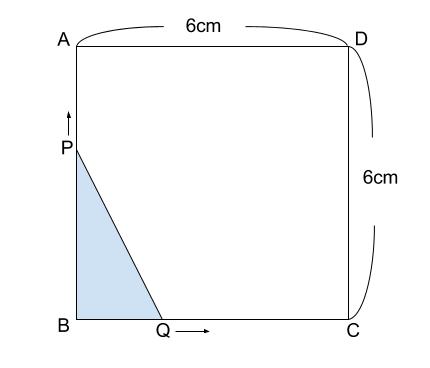
①　点 $P$ が辺 $AB$ 上を動くとき、$y$ を $x$ の式で表しなさい。
　　また、$x$ の変域を求めなさい。
② 点 $P$ が辺 $AD$ 上を動くとき、$y$ を $x$ の式で表しなさい。
　　また、$x$ の変域を求めなさい。
③　$y$ と $x$ の関係を表すグラフをかきなさい。

解説

①　点 $P$ が辺 $AB$ 上を動くとき

点$P$ は秒速 $2cm$ なので、$A$ に$6÷2=3$ (秒)でつきます。
よって、$x$ の変域は、$0 \leqq x \leqq 3$ です。

また、点 $P$ が辺 $AB$ 上を動くとき、
三角形 $BPQ$ は下図のようになります。

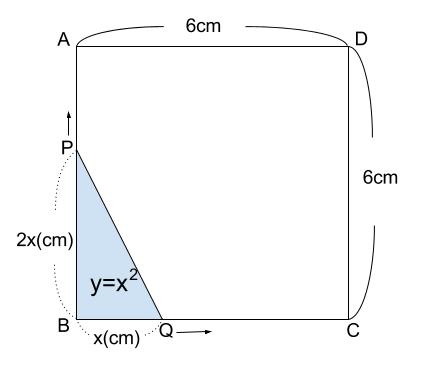
点$P$ は秒速$2cm$ で $x$ 秒進むと、$2xcm$ 進み
点$Q$ は秒速$1cm$ で $x$ 秒進むと、$xcm$ 進む。
よって、$x$ 秒後の三角形 $BPQ$ の面積 $ycm^2$ は
$y=x×2x×\displaystyle \frac{1}{2}=x^2$
よって求める式は
$y=x^2$

② 点 $P$ が辺 $AD$ 上を動くとき

$3$ 秒で $A$ に着いた点 $P$ は秒速 $2cm$ で、$D$ に向かいます。
$A$ を通過後、$6÷2=3$ (秒)で $D$ につきます。
よって、$x$ の変域は、$3 \leqq x \leqq 6$ です。

また、点 $P$ が辺 $AD$ 上を動くとき、
三角形 $BPQ$ は下図のようになります。

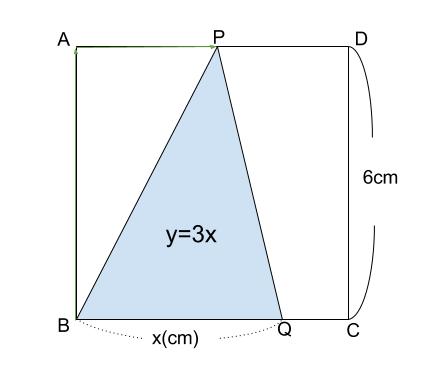
底辺 $xcm$ 、高さ $6cm$ の三角形なので、その面積は
$y=x×6×\displaystyle \frac{1}{2}=3x$
よって求める式は
$y=3x$

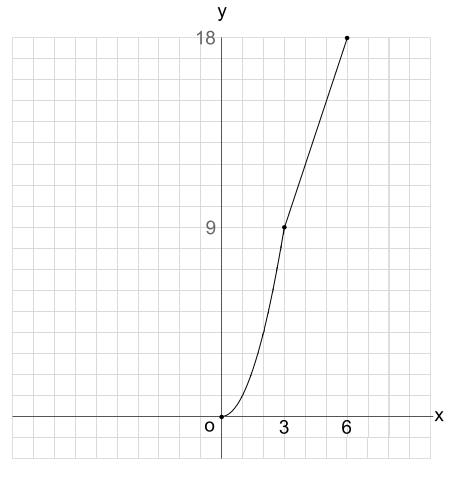
③　$y$ と $x$ の関係を表すグラフ

①、②で求めたものをグラフにします。
$y=x^2 (0 \leqq x \leqq 3)$
$y=3x (3 \leqq x \leqq 6)$
をグラフにします。

<

スポンサーリンク