すい体の高さ
空間図形において、長さを求めたいとき、
長さを求めたい線分を含む平面に注目します。
空間図形においても、平面図形の知識を活用していくのです。
例題1
下の図の円すいの高さ \(OH\) を求めなさい。
また、円すいの体積を求めなさい。
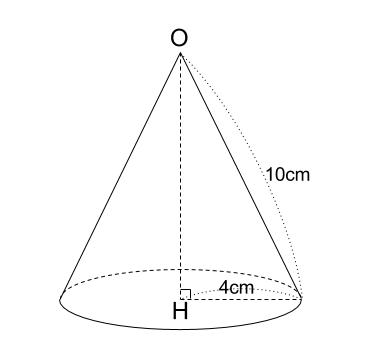
解答
下の図の水色の直角三角形に三平方の定理を用います。
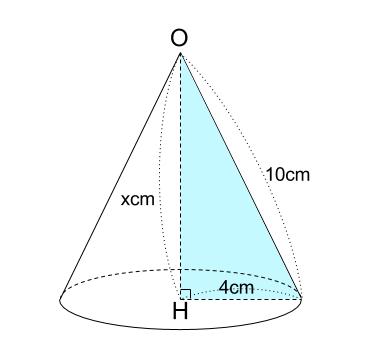
\(OH\) の長さを \(xcm\) とすると
\(x^2+4^2=10^2\)
\(x^2+16=100\)
\(x^2=100-16\)
\(x^2=84\)
\(x=±\sqrt{84}\)
\(x=±2\sqrt{21}\)
\(x \gt 0\) であるから、
\(OH\) の長さは、\(2\sqrt{21}cm\)
よって体積は、
\(4^2×\pi ×2\sqrt{21} ×\displaystyle \frac{1}{3}\)
\(=\displaystyle \frac{32\sqrt{21}}{3}\pi (cm^3)\)
例題2
下の図の正四角すいの高さ \(OH\) を求めなさい。
また、正四角すいの体積を求めなさい。
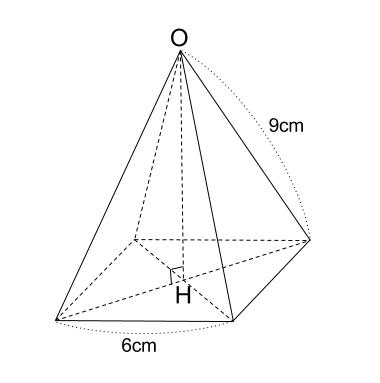
解答
下の図の水色の直角三角形 \(OAH\) に三平方の定理を用いたいですね。
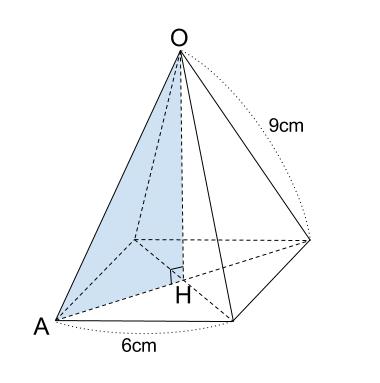
正四角すいとは、底面が正方形の四角すいです。
点 \(O\) に集まる \(4\) つの辺の長さはすべて \(9cm\) です。
また、四角すいの底面を真上から見ると、下図のようになっています。
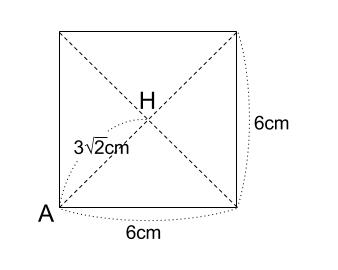
正方形の対角線の長さは \(6\sqrt{2}cm\) なので、
\(AH\) の長さは対角線の半分、 \(3\sqrt{2}cm\) です。
よって、直角三角形 \(OAH\) に三平方の定理を用います。
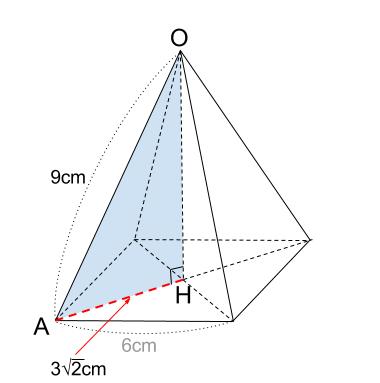
\(OH^2+(3\sqrt{2})^2=9^2\)
\(OH^2+18=81\)
\(OH^2=63\)
\(OH \gt 0\) であるから
\(OH=\sqrt{63}\)
\(=3\sqrt{7}\)
よって、正四角すいの体積は、
\(6×6×3\sqrt{7}×\displaystyle \frac{1}{3}\)
\(=36\sqrt{7}\)
