放物線と直線の交点
放物線と直線の交点は、連立方程式で求まります。
直線と直線の交点を求めるのと同じことです。
例題1
放物線 \(y=x^2\) と直線 \(y=x+2\) の交点の座標を求めなさい。
解説
放物線 \(y=x^2\) と直線 \(y=x+2\) の交点を点 \(P\) とします。
点 \(P\) の \(x\) 座標を \(p\) とすると、
点 \(P\) は放物線 \(y=x^2\) 上の点なので、\(P(p,p^2)\) と表せます。
また、点 \(P\) は直線 \(y=x+2\) 上の点なので、\(P(p,p+2)\) と表せます。
どちらも同じ点 \(P\) の座標なので、 \(y\) 座標は等しいわけです。
つまり、\(p^2=p+2\) です。
この \(2\) 次方程式を解けば、交点 \(P\) の \(x\) 座標 \(p\) が求まります。
\(p^2=p+2\)
\(p^2-p-2=0\)
\((p+1)(p-2)=0\)
より、
\(p=-1,2\)
あれ、 \(2\) つ求まりましたね。
そうです、交点は \(2\) つなのです。
求まった \(x\) 座標 \(-1,2\) をそれぞれ直線 \(y=x+2\) に代入して
座標を求めます。
\((-1,1)\) と \((2,4)\) です。
もちろん \(x\) 座標 \(-1,2\) を放物線 \(y=x^2\) に代入して
座標を求めてもOKです。
下図のようになっています。
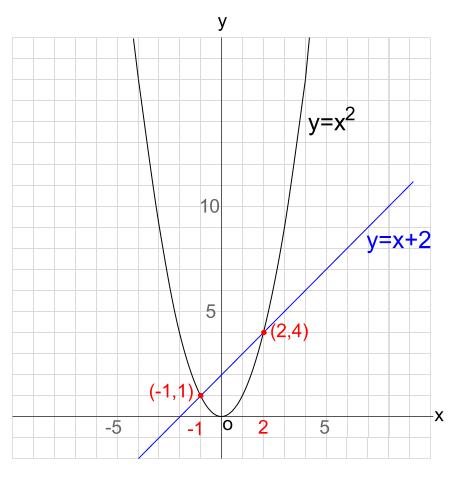
交点の求め方・まとめ
交点の座標は \(2\) 次方程式を解くことで得られました。
あの式って結局、放物線 \(y=x^2\) と直線 \(y=x+2\) の式を連立したものです。
つまり、
\(y=x^2\)
\(y=x+2\)
を連立して解くと、交点の座標が求まるということです。
\(y\) を消せば、 \(x^2=x+2\) という \(2\) 次方程式になります。
さきほど解いた \(2\) 次方程式と同一のものですね。
交点 とは、上の \(2\) つの式を満たす \(x\) と \(y\) を座標に持つのですから、
連立すれば求まるのは当たり前ですね!
例題2
放物線 \(y= \displaystyle \frac{1}{2} x^2\) と直線 \(y=x+4\) の交点の座標を求めなさい。
解説
交点を求めるには、式を連立します。
\(y= \displaystyle \frac{1}{2} x^2\) と \(y=x+4\) から \(y\) を消すと
\( \displaystyle \frac{1}{2} x^2=x+4\)
両辺を \(2\) 倍すると
\(x^2=2x+8\)
\(x^2-2x-8=0\)
\((x+2)(x-4)=0\)
よって
\(x=-2,4\)
これを \(y=x+4\) に代入して、
\((-2,2),(4,8)\) と交点が求まりました。
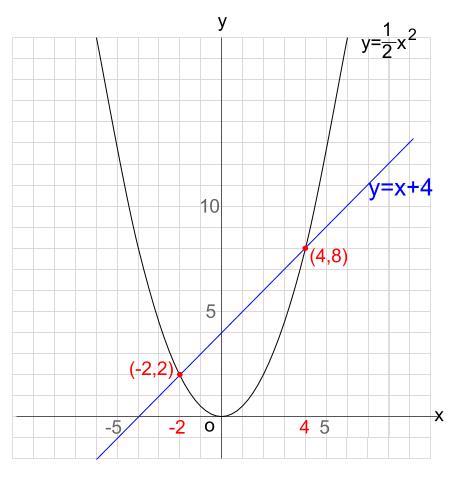
※放物線と直線は、交わらないこともあります。
\(1\) 点でのみ交わることもあります。このとき、放物線と直線は接するといい、
接している点を接点といいます。交点とはいいません。
スポンサーリンク
