1次式×1次式が主役
式の展開は、「ひたすら順番にかけ算をすること」
であることを確認してきました。
この式の展開の中で、非常によく使われるものは
「公式」として用いられています。
どのような式が、非常によく使われるのでしょうか。
ずばり・・・
\((x の1次式で、xの係数が1のもの)\)\(×(x の1次式で、xの係数が1のもの)\)
です。
具体例を見た方が理解が速いでしょう。
\((x+1)(x+2)\)
\((x-1)(x+2)\)
\((x-1)(x-2)\)
\((x+1)(x-1)\)
\((x+4)(x+4)=(x+4)^2\)
などです。
なぜこれらが、、非常によく使われるものなのか。
これもずばり教えてしまいましょう。
\(2\) 次方程式を解くための基礎の土台となるから!
へーそうなんだ・・・としか言いようがないですね。
すぐに \(2\) 次方程式の学習に到達しますからお楽しみに!!
この単元は、基礎の土台です。
九九みたいなもので、素早くできないと使い物にならない
というような類のものです。
どんどん練習して、素早く展開ができるようになりましょう。
乗法公式
第 \(1\) の公式は以下のものです。
\((x+a)(x+b)=x^2+(a+b)x+ab\)
一体どのようにこの公式を使うの?って思いますよね。
\(x\) の \(1\) 次の項は、和
定数項は、積
になっているよ!
という公式なのです。
具体例をみて学習していかないと話になりません。
下の例を見ていきましょう。
例
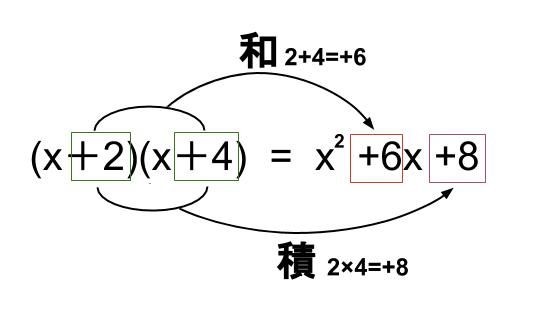
\((x+2)(x+4)\)
\((x+2)(x+4)\)
\(=x^2+(2+4)x+2×4\)
\(=x^2+6x+8\)
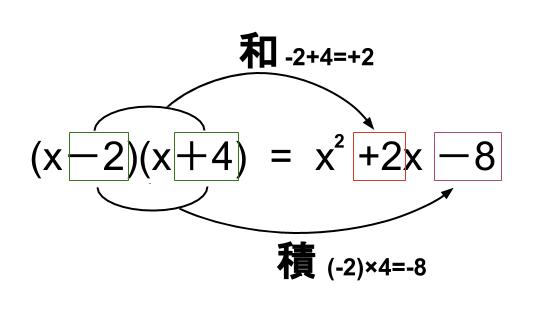
\((x-2)(x+4)\)
\((x-2)(x+4)\)
\(=x^2+\{(-2)+4\}x+(-2)×4\)
\(=x^2+2x-8\)
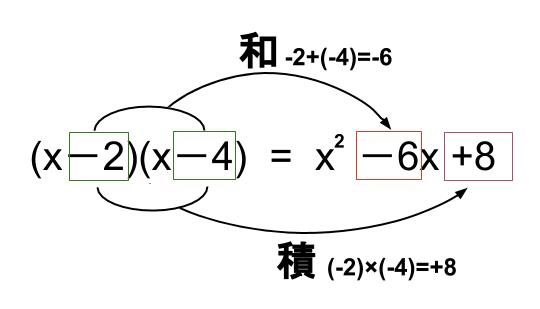
\((x-2)(x-4)\)
\((x-2)(x-4)\)
\(=x^2+\{(-2)+(-4)\}x+(-2)×(-4)\)
\(=x^2-6x+8\)
どうしても不安になったら、普通に \(4\) 回かけ算をして展開をしてもかまいません。
練習を積んでいくうちに、慣れて使いこなせるようになっていきます。
平方の公式
\((x+a)^2=x^2+2ax+a^2\)
\((x-a)^2=x^2-2ax+a^2\)
見ての通り、同じ \(1\) 次式を \(2\) 回かけたときに使います。
これも具体例での学習につきます。
例
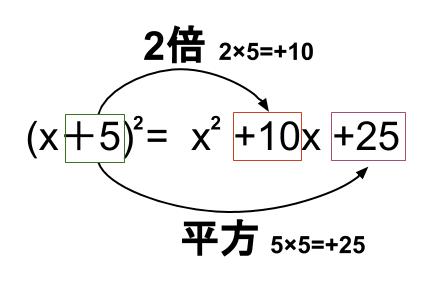
\((x+5)^2\)
\((x+5)^2\)
\(=x^2+2×5x+5^2\)
\(=x^2+10x+25\)
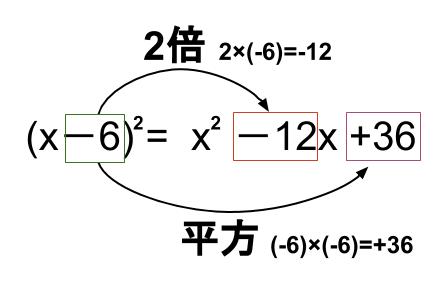
\((x-6)^2\)
\((x-6)^2\)
\(=x^2+2×(-6)x+(-6)^2\)
\(=x^2-12x+36\)
和と差の積の公式
\((x+a)(x-a)=x^2-a^2\)
定数項の符号だけが違う \(1\) 次式の積のときに用います。
これも具体例での学習につきます。
例
\((x+7)(x-7)\)
\((x+7)(x-7)\)
\(=x^2-7^2\)

まとめ 公式の適用について
公式に習熟することで、素早い展開が可能になります。
しがし、公式を忘れた、符号はあやふや、などのときは、
普通に分配法則を用いて展開をすれば、それでOKです。
上の3種類の公式も、分配法則によって得られた結果を利用しているだけです。
また、いずれの公式も適用できないときもあります。
そのようなときはもちろん、普通に分配法則を用いて展開をするのです。
スポンサーリンク
