【中学数学】因数分解・乗法公式

乗法公式による因数分解

因数分解とは展開の逆操作である！

さて、様々な展開公式を学習してきたわけですから、
それがそっくりそのまま因数分解の公式となって再登場するわけです。

$x^2+(a+b)x+ab=(x+a)(x+b)$

まさに展開の逆ですが・・・
因数分解は展開より難しいです。
今まで以上にしっかりと練習を積んでいきましょう。

例題１

次の式を因数分解しなさい。
$x^2+5x+6$

解説

この因数分解は「公式にあてはめて計算！」
のような単純な方法ではできません。

和と積から、もとの $2$ つの数を探し出す「数調べゲーム」なのです。
展開のとき、
$x$ の $1$ 次の項の係数が「和」
定数項が「積」
になったことが記憶に新しいですね。

つまり、この例題においては、

和が $+5$、積が $+6$ になる $2$ つの数を見つけるのです。

どうやって見つけるのでしょうか・・・
ひたすら調べるしかないのです。

因数分解の手順

積が $+6$ になる $2$ つの整数の組を書き出します。

その中で、和が $+5$ になるものを探します。

見つかりましたね。

$2,(+2)$ と $3,(+3)$ です。
よって、
$x^2+5x+6=(x+2)(x+3)$

例題２

次の式を因数分解しなさい。
$x^2-10x+9$

解説

積が $+9$ になる $2$ つの整数の組を書き出します。
その中で、和が $-10$ になるものを探します。

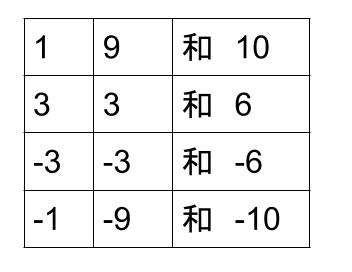
見つかりましたね。

$-1$ と $-9$ です。
よって、
$x^2-10x+9=(x-1)(x-9)$

例題３

次の式を因数分解しなさい。
$x^2+6x-16$

解説

積が $-16$ になる $2$ つの整数の組を書き出します。
その中で、和が $+6$ になるものを探します。

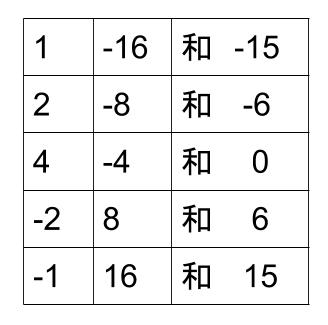
見つかりましたね。

$+8$ と $-2$ です。
よって、
$x^2+6x-16=(x-2)(x+8)$

例題４

次の式を因数分解しなさい。
$2x^2-6x-20$

解説

まず、式全体が共通因数の $2$ でくくれます。
$2x^2-6x-20=2(x^2-3x-10)$

次に、（　）の中がさらに因数分解できるか考えます。

積が $-10$ になる整数を $2$ つ書き出します。
その中で、和が $-3$ になるものを探します。

$2$ と $-5$ が見つかります。
よって、
$2x^2-6x-20$
$=2(x^2-3x-10)$
$=2(x+2)(x-5)$

スポンサーリンク

• 次のページ 因数分解・平方の公式、和と差の公式
• 前のページ 因数分解・共通因数でくくる