【中学数学】平方根の導入・その２

平方根の具体的な数値

数直線で見てみよう！

$\sqrt{2}$ や $\sqrt{3}$ が、結局どのような数なのか、実感を持つために
数直線上で見ておきましょう。

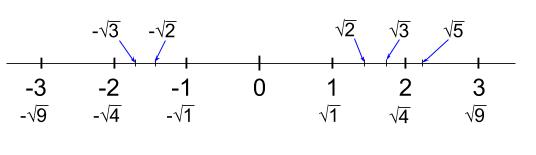
平方根の大小関係ですが、根号の中の数の大小関係を見ればよいことがわかります。
$\sqrt{2}$　＜　$\sqrt{3}$ です。

√Ｎって結局いくつなの？

$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$ のおよその値は覚えておきたいです（必須とは言いませんが）。
小数点以下第 $3$ 位までで十分ですが、下記のような非常に覚えやすいゴロ合わせがあります。
$\sqrt{2}=1.41421356$・・・ひとよひとよにひとみごろ（一夜一夜に人見頃）
$\sqrt{3}=1.7320508$・・・ひとなみにおごれや（人並みに奢れや）
$\sqrt{5}=2.2360679$・・・ふじさんろくおうむなく（富士山麓オウム鳴く）

ところで $\sqrt{4}$ がぬけています
$\sqrt{4}=2$ ですね。
このように整数値になる値は非常に重要です。
当然ですが、平方数の平方根が整数となります。
平方数とは$N^2$（Nは整数）で表される数です。

$1$ の平方根は $±1$
$4$ の平方根は $±2$
$9$ の平方根は $±3$
以下続く

これは、$1^2$、$2^2$、$3^2$、$4^2$、・・・
と平方数を順に覚えることに相当します。
九九は暗記していますし、、$10×10=100$ も楽勝ですので
$11^2 =121$、$12^2 =144$、$13^2=169$、$14^2=196$、$15^2=225$、
の5つを新しく覚えておくといいでしょう。

また、以下の２つも頭にいれておきましょう。
・$０$ の平方根は $０$
・負の数の平方根はない

例題

根号を用いて表す方法に慣れていきましょう。
次の問いに答えなさい。
（１）$3$ の平方根を求めなさい。
（２）$\sqrt{81}$ の値は？

解答

（１）
$3$ の平方根は？　⇒　$x=±\sqrt{3}$
ですね。正と負に１つずつです。

（２）
$\sqrt{81}$ の値は？　⇒　$±\sqrt{81}=±9$
この答えおかしいのですが・・・
わかりますか？

$\sqrt{81}$ は正の数です。
よって、$\sqrt{81}=9$
です。

意識すべきこと！

プラスとマイナスの2つを同時に答えるべきなのか、
正負、符号が確定している値なのか、
これを意識することが大事です。

スポンサーリンク

• 次のページ 平方根の計算ルール
• 前のページ 平方根の導入・その１