【中学数学】 $y=ax^2$ （2乗に比例）導入

$y=ax^2$ 2乗に比例

$y$ が $x$ の関数であり、 $x$ と $y$ の間に
$y=ax^2$
という関係式が成り立つとき、$y$ は $x$ の $2$ 乗に比例するという。
ただし、$a$ は $0$ でない定数で、比例定数といいます。

「$y$ は $x$ の $2$ 乗に比例する」と問題文にあれば、すぐさま、$y=ax^2$ とかくようにしましょう。
暗記ですよ、これは。

$a$ はさまざまな値をとるので、これから学習するのは例えば、
$y=x^2$
$y=3x^2$
$y=-x^2$
などの関数です。

2次関数とは

$y=ax^2$ は、$2$ 次関数ともいわれます。
$2$ 次関数とは、
$y=x^2$
$y=-3x^2+1$
$y=x^2+x$
$y=\displaystyle \frac{1}{3}x^2-2x+3$
のような，$y=x の2次式$ となるものです。

中学 $3$ 年では、この中で $y=ax^2$ の形のものだけを学習します。
$2$ 次関数すべてを学習するのは、高校生になってからです。

注意
$y=\displaystyle \frac{a}{x^2}$
は $2$ 次関数ではありません。
$x^2$ が分母にあるとき、$x$の$-2$乗なのです。
くわしくは高校で学習します。

$y=ax^2$　（2乗に比例）の特徴

$y=ax^2$ について、$x$ の値を $n$ 倍すると、$y$ の値は $n^2$ 倍になる。

例
$y=2x^2$

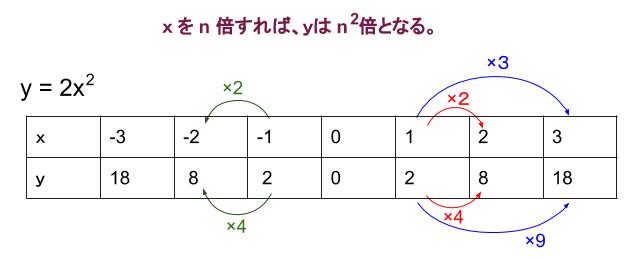
$y=ax^2$　（2乗に比例）の具体例

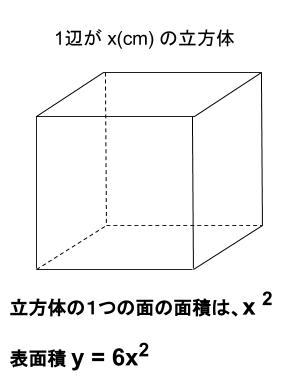
$1$ 辺が $xcm$の立方体の表面積を $ycm^2$する。

このとき、$y$ と $x$ の間には
$y=6x^2$
という関係式が成立します。

例題 1

次の場合について、$y$ を $x$ の式で表し、 $y$ が$x$ の $2$ 乗に比例するものには〇、そうでないものには×をかきなさい。
（１）半径が $xcm$ の円の面積 $ycm^2$
（２）底辺が $xcm$ 、高さが $2xcm$ の三角形の面積 $ycm^2$
（３）たて$xcm$ 、面積が $20cm^2$ の長方形のよこの長さ $ycm$

解説

$y$ が$x$ の $2$ 乗に比例するとは、$y$ を $x$ の式に表した時に
$y=ax^2$ の式になることです。
これは覚えてしまいましょう。

（１）半径が $xcm$ の円の面積 $ycm^2$

（１）円の面積＝円周率×半径の $2$ 乗なので、
$y= \pi x^2$
これは $y$ が $x$ の $2$ 乗に比例するので、〇です。

（２）底辺が $xcm$ 、高さが $2xcm$ の三角形の面積 $ycm^2$

（２）三角形の面積＝底辺×高さ×$\displaystyle \frac{1}{2}$ なので、
$y= x×2x × \displaystyle \frac{1}{2}$
これは $y$ が $x$ の $2$ 乗に比例するので、〇です。

（３）たて$xcm$ 、面積が $20cm^2$ の長方形のよこの長さ $ycm$

（３）長方形の面積＝たて×よこ　　なので、
$20= xy$
これは $y$ が $x$ の $2$ 乗に比例しないので、×です。

例題２

$y$ が $x$ の $2$ 乗に比例し、$x=6$ のとき、$y=18$ である。このとき次の問いに答えなさい。
（１）$y$ を $x$ の式で表しなさい。
（２）$x=-3$ のときの $y$ の値を求めなさい。
（３）$y=32$ のときの $x$ の値を求めなさい。

解説

$y$ が $x$ の $2$ 乗に比例　とあるので、即座に $y=ax^2$ とします。

（１）$y$ を $x$ の式で表しなさい

（１）$x=6$ のとき $y=18$ なので、これを $y=ax^2$ に代入して、$a$ を求めます。
$18=a×6^2$
よって
$a= \displaystyle \frac{1}{2}$
です。
つまり、求める式は $y=\displaystyle \frac{1}{2}x^2$

（２）$x=-3$ のときの $y$ の値を求めなさい

(1)で求めた式に、$x=-3$ を代入して、このときの$y$ を求めます。
$y=\displaystyle \frac{1}{2}×(-3)^2$
よって
$y=\displaystyle \frac{9}{2}$
です。

（３）$y=32$ のときの $x$ の値を求めなさい

(1)で求めた式に、$y=32$ を代入して、このときの$x$ を求めます。
$32=\displaystyle \frac{1}{2}x^2$
よって
$x^2=64$
$x= ±8$
です。
$x$ は $2$ つの値がでてきましたね。

スポンサーリンク

• 次のページ $y=ax^2$ のグラフをかく