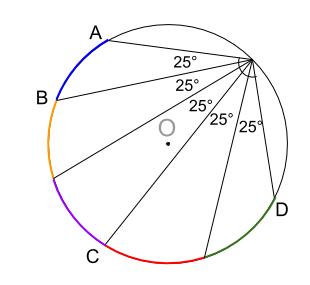
例題1
下の図の角 \(x\),\(y\) の大きさを求めなさい。
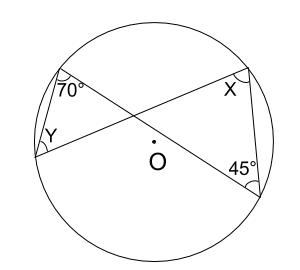
解説
同じ弧に対する円周角は等しいので、
\(\angle X=70°\)
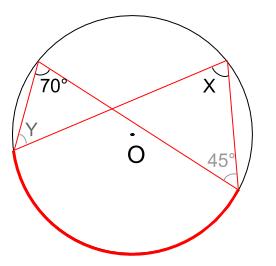
同様に、同じ弧に対する円周角は等しいので、
\(\angle Y=45°\)
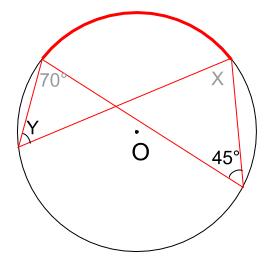
例題2
下の図の角 \(x\) の大きさを求めなさい。
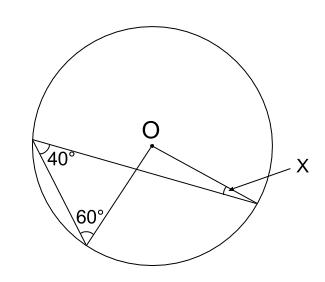
解説
同じ弧に対する円周角は中心角の半分なので、下図の赤い弧の中心角は \(80°\)
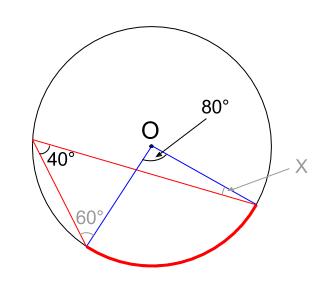
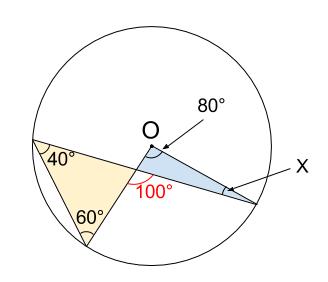
あとは、色をつけた \(2\) つの三角形の角に着目すればよいです。
左の黄色い三角形の外角より、赤い角の大きさは \(100°\)
これは、右の青い三角形の外角でもあるので、\(\angle X=100-80=20°\)
例題3
下の図の角 \(x\),\(y\) の大きさを求めなさい。
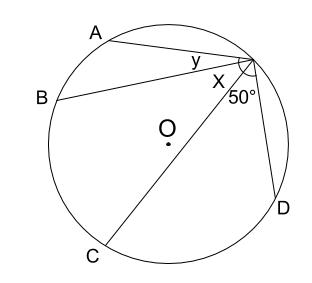
ただし、\(\stackrel{ \Large \frown }{ AB }×2=\stackrel{ \Large \frown }{ BC }=\stackrel{ \Large \frown }{ CD }\)
解説
等しい弧に対する円周角は等しいので、
\(\angle X=50°\)
弧の長さと、それに対する円周角の大きさは比例するので、
弧の長さが半分になれば、円周角の大きさも半分になります。
よって、\(\angle Y=50÷2=25°\)