【中学数学】 $y=ax^2$ 図形との融合問題 | 中学数学の無料オンライン学習サイトchu-su-

座標平面上の三角形

関数 $y=ax^2$ と図形問題の融合として、非常によく出題される定番パターンを学習します。
解法をきちんと理解した上で、しっかりとその流れを暗記してしましましょう。

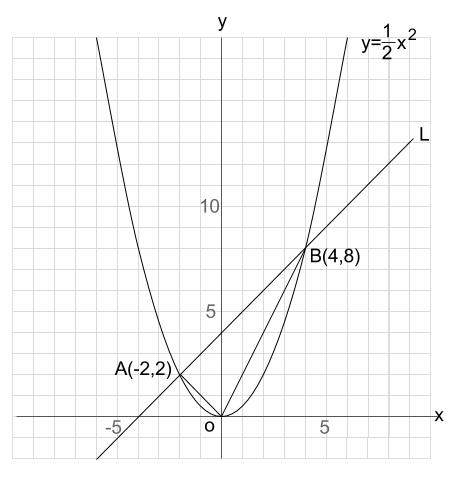
下の図で、$A,B$ は直線 $L$ と関数 $y=\displaystyle \frac{1}{2}x^2$ との交点である。
次の問いに答えなさい。

（１）△$OAB$ の面積を求めなさい。　
（２）原点を通り、 △$OAB$ の面積を $2$ 等分する直線の式を求めなさい。　　

$中学数学・高校受験chu-su- 2次関数　図形融合　図１$

（１）△ $OAB$ の面積は、下図のように分けて考えるのが楽です。

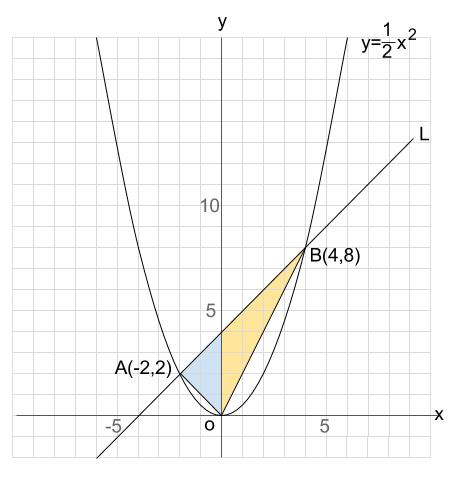
$中学数学・高校受験chu-su- 2次関数　図形融合　図２$

よって、直線 $L$ の切片がいくつなのか求めたいですね。
そのために、直線 $L$ の式を求めましょう。
直線 $L$ は、$2$ 点 $(-2,2)$、$(4,8)$ を通るので、
$y=x+4$
と求まります。

よって、切片は $4$ なので、下図のように $2$ つの三角形の面積が求まります。

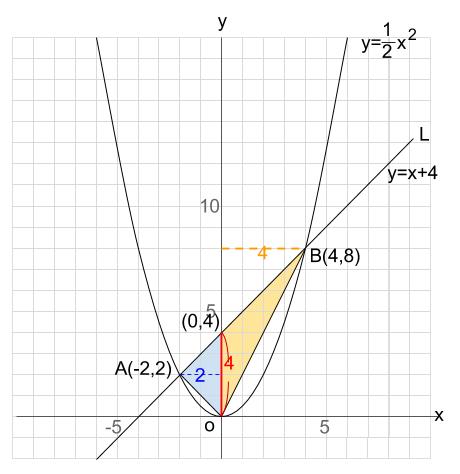
$中学数学・高校受験chu-su- 2次関数　図形融合　図3$

よって
$4×(2+4)÷2=12$

（2）頂点を通る直線で三角形の面積を $2$ 等分するのは、下図のようになります。

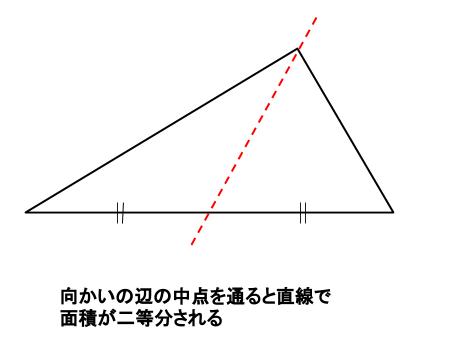
$中学数学・高校受験chu-su- 2次関数　図形融合　図４$

よって、△ $OAB$ の面積が、原点を通る直線で $2$ 等分されるとは、下図のようになります。
つまり、もとめる直線は $AB$ の中点を通るのです！！

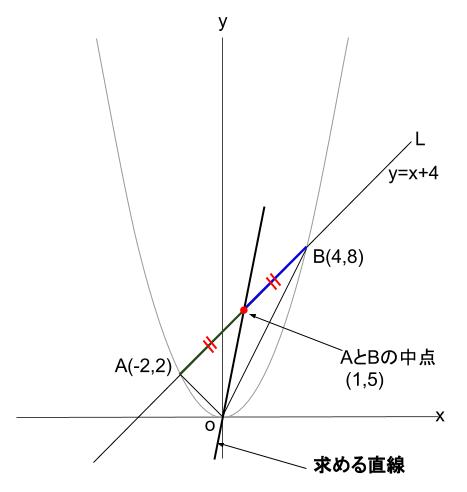
$中学数学・高校受験chu-su- 2次関数　図形融合　図５$

$A$ と $B$ の中点の求め方は覚えていますか？
$A$ と $B$ の $x$ 座標の平均が、中点の $x$ 座標
$A$ と $B$ の $y$ 座標の平均が、中点の $y$ 座標
です。

つまり、$A$ と $B$ の中点の座標は
$(\displaystyle \frac{-2+4}{2}$, $\displaystyle \frac{2+8}{2}) = (1,5)$

よって、求める直線は、原点と $(1,5)$ を通る直線なので、
$y=5x$
と求まります。