相似な図形の面積比
相似な図形の面積の比は「相似比の \(2\) 乗の比」になります。
つまり、相似比 \(a:b\) の図形の面積の比は \(a^2:b^2\) です。
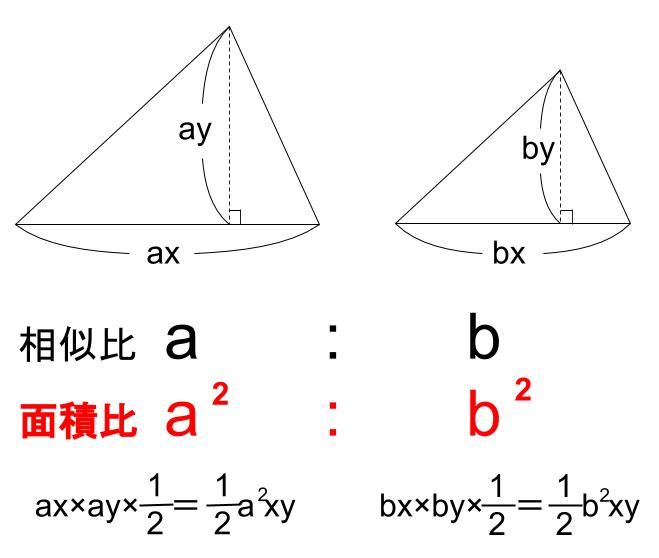
なので
面積の比は \(a×a:b×b\) となるわけです。
もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも
相似な図形ならば、面積比は相似比の \(2\) 乗の比が成り立ちます。
例題1
下の図で \(DE /\!/ BC\) のとき、
三角形 \(ADE\) と台形 \(DBCE\) の面積の比を求めなさい。
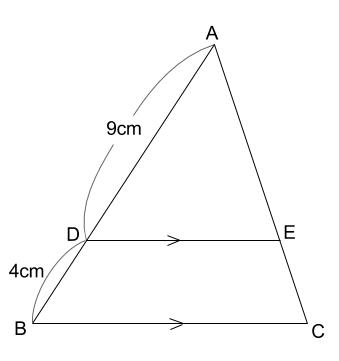
\(DE /\!/ BC\) なので、「ピラミッド型相似」です。
小さい三角形を横にぬき出して考えましょう。

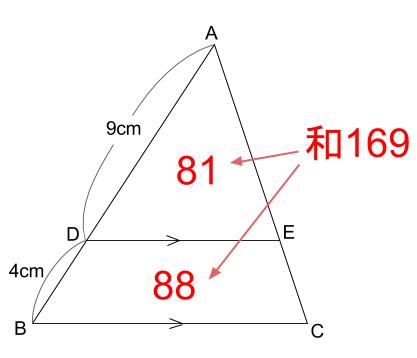
相似比は \(9+4:9=13:9\) です。
よって面積比は、\(13^2:9^2=169:81\) です。
つまり、台形 \(DBCE\) の面積は、\(169-81=88\) となります。
※厳密には比なので、台形 \(DBCE\) の面積は三角形 \(ABC\) の \(\displaystyle \frac{81}{169}\) というのが正しい。
よって、三角形 \(ADE\) と台形 \(DBCE\) の面積の比は
\(81:88\)
と求まります。
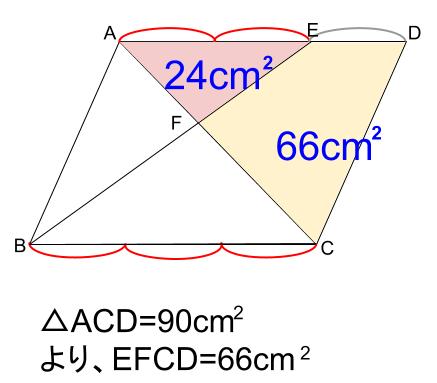
例題2
下の図で \(ABCD\) は平行四辺形で、点 \(E\) は \(AD\) を \(3\) 等分する点のうち、 \(D\) に近いほうの点で、点 \(F\) は \(AC\) と \(EB\) の交点です。\(ABCD\) の面積が \(180cm^2\) のとき、四角形 \(EFCD\) の面積を求めなさい。
解説
平行な線がある図形ですので、「砂時計型」と「ピラミッド型」
に敏感に反応したいです。
本問は、「砂時計型」が見えて欲しい問題です。
相似比は \(2:3\) ですね。
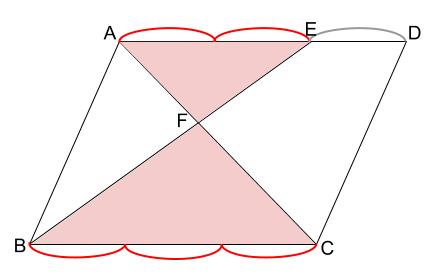
よって、\(AF:FC=2:3\) なので、
\(\triangle ABF : \triangle FBC=2:3\) です。
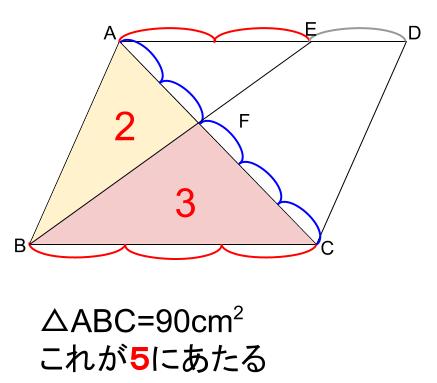
\(\triangle ABC\) は平行四辺形の半分なので、
その面積は \(90cm^2\) です。
\(\triangle ABF\) は \(\triangle ABC\) の \(\displaystyle \frac{2}{2+3}\) なので
\(\triangle ABF=90×\displaystyle \frac{2}{2+3}=36(cm^2)\)
さらに、「砂時計型相似」より、\(BF:EF=3:2\) なので
\(\triangle AFE\) は \(\triangle ABF\) の \(\displaystyle \frac{2}{3}\) となります。
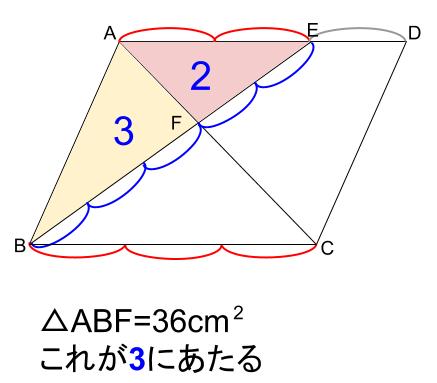
\(\triangle AFE=36×\displaystyle \frac{2}{3}=24(cm^2)\)
四角形 \(EFCD\) の面積は、\(\triangle ACD\) から \(\triangle AFE\) を引けばよいので、
\(90-24=66(cm^2)\)
と求まります。