中点連結定理
\(\triangle ABC\) において、\(M,N\) がそれぞれ \(AB,AC\) の中点のとき、
\(MN /\!/ BC\)
\(MN=\displaystyle \frac{1}{2}BC\)
が成り立つ。
これを中点連結定理といいます。
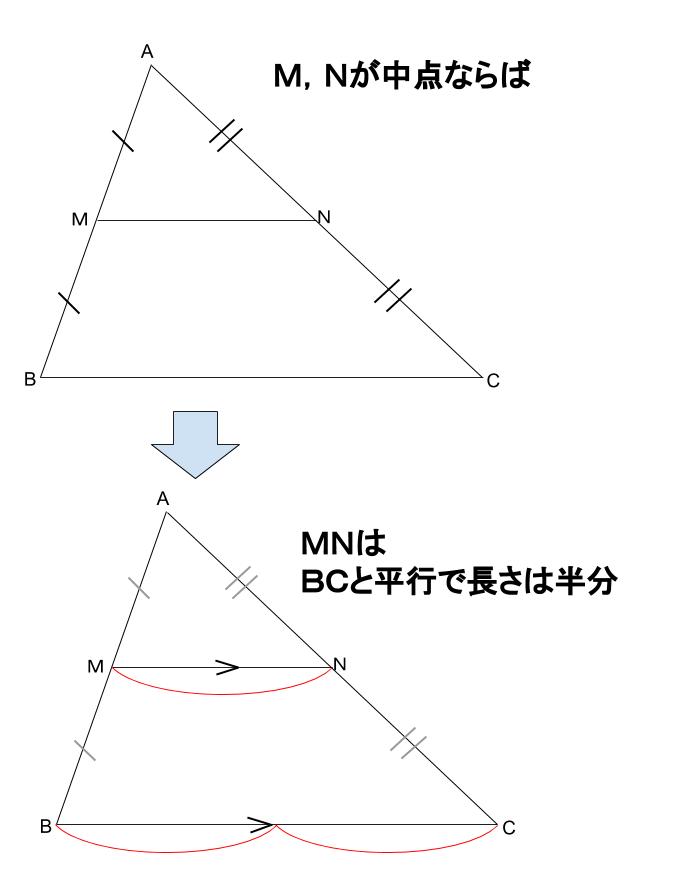
逆も成り立ちます。
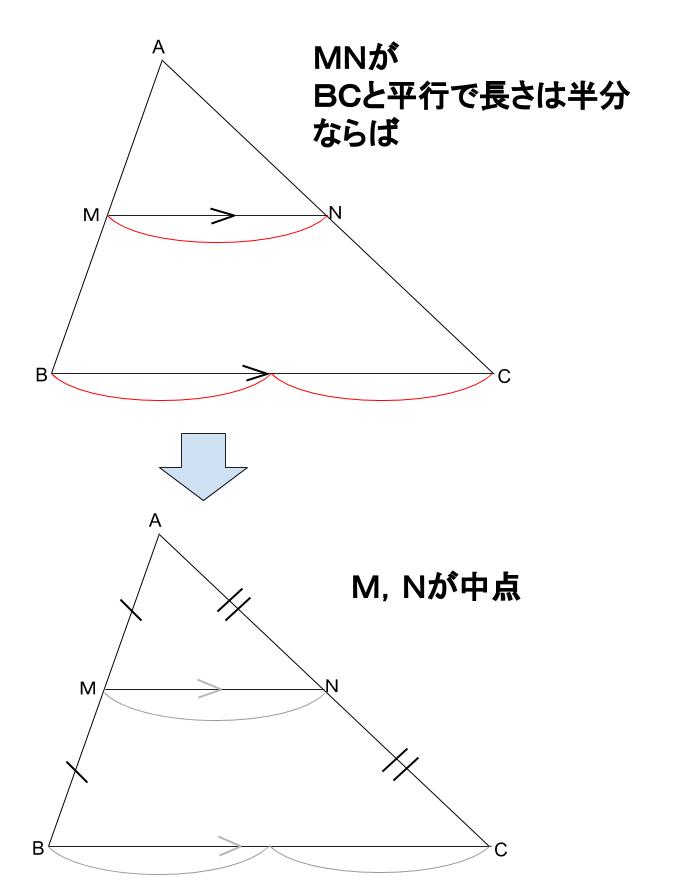
あまり深く考えないでOKですよ。
ただのピラミッド型じゃないですか・・・
中点連結定理などという、たいそうな名前がついた定理ですが、
以前に学習した、
「ピラミッド型三角形」の相似比が \(1:2\) のケースです。
はっきり言って、こんな定理いらないです・・・
きちんと相似を理解していれば。
ただし、一応知っておいてくださいね。
こうやって名前が付けられている以上、
「中点連結定理」と言われて、何のことかわからないと
困ります。
それに、例題2で見ますが、
やはり、「中点連結定理」があると便利なときもあるんです。
例題1
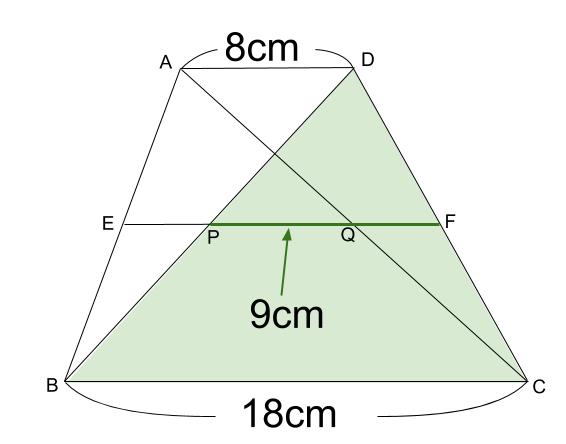
下の図のように、\(AD /\!/ BC\) の台形において、\(AD /\!/ EF\)
\(AE=EB\) のとき、\(PQ\) の長さを求めなさい。
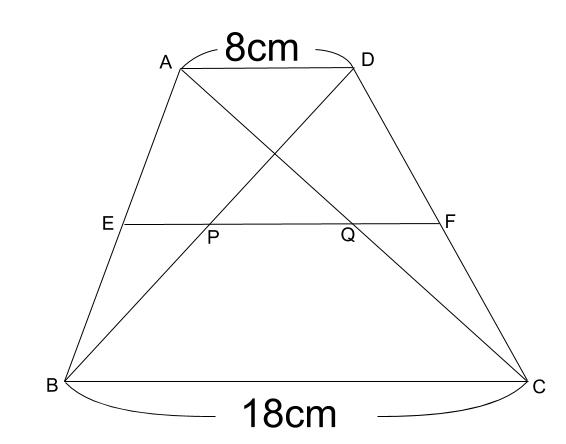
解説
ピラミッド型を利用すれば良いだけです。
下図のように、相似比が \(1:2\) のピラミッド型が \(2\) つあります。
よって、
\(EQ=18×\displaystyle \frac{1}{2}=9\)
\(QF=8×\displaystyle \frac{1}{2}=4\)
と求まります。
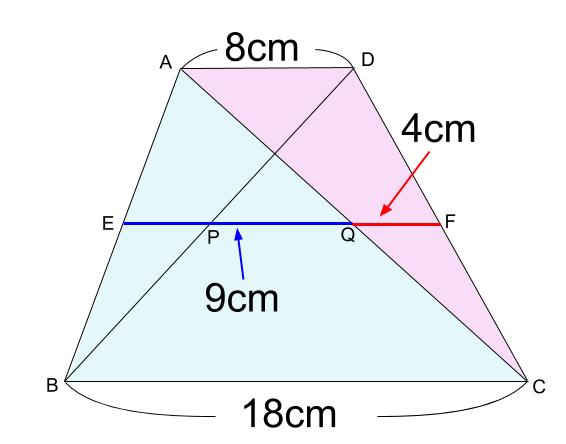
このような、ピラミッド型で相似比が \(1:2\) のとき
三角形 \(ABC\) において「中点連結定理より」
\(EQ=18×\displaystyle \frac{1}{2}=9\)
という特殊な言い回しで計算することがあります。
同様に、
三角形 \(CAD\) において「中点連結定理より」
\(QF=8×\displaystyle \frac{1}{2}=4\)
です。
「中点連結定理」など、ただそれだけの話です。
難しく考えないでください。
同様に、下図のピラミッド型にも着目することで、
「中点連結定理より」
\(PF=18×\displaystyle \frac{1}{2}=9\)
より、
\(PQ=PF-QF=9-4=5(cm)\)
例題2
四角形 \(ABCD\) の \(4\) 辺 \(AB,BC,CD,DA\) の中点をそれぞれ、\(P,Q,R,S\) とすると、四角形 \(PQRS\) は平行四辺形であることを証明しなさい。
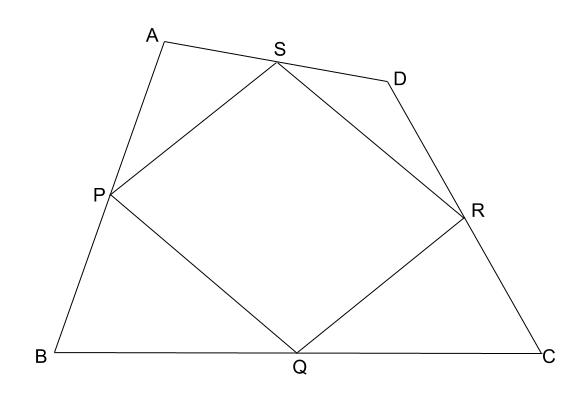
解説
これは「中点連結定理」が大活躍する代表例です。
解説を読んで「なるほど」と思ってください。
下図のように、対角線 \(BD\) を引くことで、
相似比 \(1:2\) のピラミッド型が \(2\) つできます。
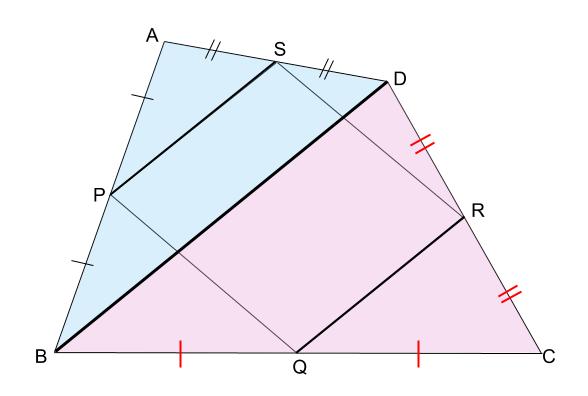
水色のピラミッド型三角形に着目すれば
\(PS=BD×\displaystyle \frac{1}{2}\)
かつ \(PS /\!/ BD\)
です。
これは、「中点連結定理より」と根拠をかけばOKです。
「証明で中点連結定理が使えるとき」
これこそが中点連結定理が活躍する唯一の機会といってよいでしょう。
「中点連結定理より」とかかないならば、
\(\triangle APS \backsim \triangle ABD\) を示し、
その角度から、平行線の錯角で \(PS /\!/ BD\) を示す必要があります。
これらをすべて「既知のことですよね」として
省略してしまってよいキーワードが
「中点連結定理より」なのです。
同様に薄い紫色のピラミッド型三角形に着目すれば
「中点連結定理より」
\(QR=BD×\displaystyle \frac{1}{2}\)
かつ \(QR /\!/ BD\)
です。
以上より、\(PS=QR\)
かつ\(PS /\!/ QR\)
なので、\(1\) 組の対辺が平行でその長さが等しいから四角形 \(PQRS\) は平行四辺形である
といえます。
これを、証明の文としてまとめればOKです。
証明文
対角線 \(BD\) をひくと
三角形 \(ABD\) において、点 \(P,S\) はそれぞれ \(AB,AD\) の中点なので
中点連結定理により、
\(PS=BD×\displaystyle \frac{1}{2}\) かつ \(PS /\!/ BD\) ・・・①
同様に
三角形 \(CBD\) において、点 \(Q,R\) はそれぞれ \(CB,CD\) の中点なので
中点連結定理により、
\(QR=BD×\displaystyle \frac{1}{2}\) かつ \(QR /\!/ BD\) ・・・②
①、②より
\(PS=QR\) かつ \(PS /\!/ QR\)
よって、 \(1\) 組の対辺が平行でその長さが等しいから四角形 \(PQRS\) は平行四辺形である。
