三角形の相似条件
\(2\) つの三角形があり、それらが相似であるかどうかを判定する。
そのために、三角形の相似条件があります。
相似条件
- \(3\) 組の辺の比がそれぞれ等しい
- \(2\) 組の辺の比とその間の角がそれぞれ等しい
- \(2\) 組の角がそれぞれ等しい
三角形の合同条件というものを、中学 \(2\) 年生で学習しましたね。
相似条件は、それとそっくりです。
なぜなら、相似比が \(1:1\) のものを「合同」と呼んでいるからです。
「合同」は「相似」の中の一部なのです。
合同のとき、辺の長さが等しいという条件が必要でしたが、相似においては辺の長さが等しい必要はありません。
三角形 \(ABC\) と三角形 \(DEF\) が相似ならば、
\(3\) つの辺がすべて同じ倍率で縮小(拡大)されているわけです。
つまり、合同条件では「辺の長さが等しい」だった箇所が、相似条件では「辺の比が等しい」になっています。
①3組の辺の比が等しい
合同条件では、「\(3\) つの辺がそれぞれ等しい」でした。
それはつまり、長さが \(a\),\(b\),\(c\) の \(3\) 本の棒を \(P\) くんと \(Q\) くんのそれぞれに与え、
その棒を辺とする三角形を作らせるとき、\(P\) くんと \(Q\) くんのつくる三角形が必ず合同になるということです。
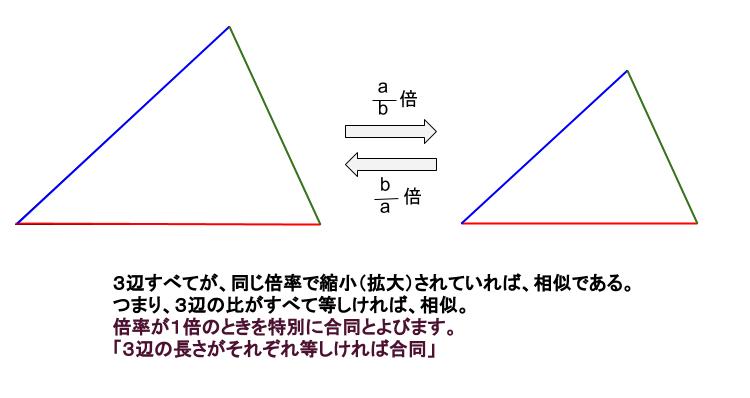
相似条件では、「\(3\) 組の辺の比がそれぞれ等しい」となります。
\(P\) くんにあげた \(3\) 本の棒にすべて同じ倍率で長さを変えた棒を \(Q\) くんに与えます。
このとき、\(P\) くんと \(Q\) くんのつくる三角形が必ず相似になるということです。
②2組の辺の比とその間の角がそれぞれ等しい
合同条件では、「\(2\) 辺とその間の角がそれぞれ等しい」でした。
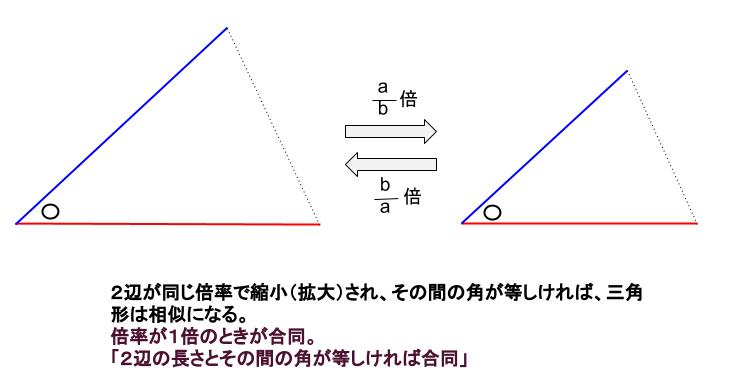
相似条件では、「\(2\) 組の辺の比とその間の角がそれぞれ等しい 」となります。
\(2\) 辺の比ともに \(1:1\) のときが合同。
\(2\) 辺の比が、そろっていれば相似です。
つまり、\(2\) 辺が同じ倍率で縮小(拡大)されていれば同じ形(相似)になるということです。
③2組の角がそれぞれ等しい
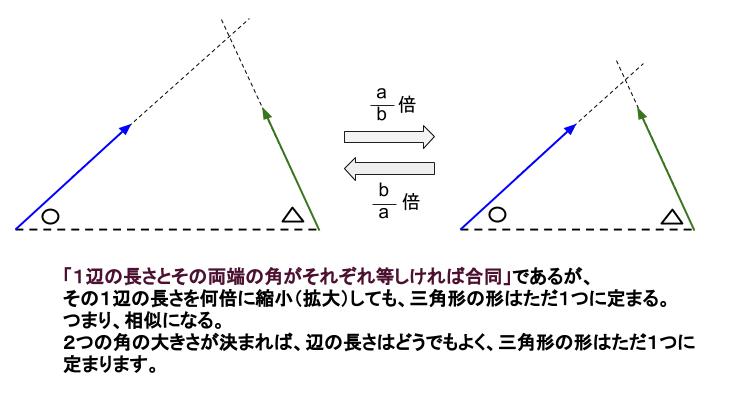
合同条件では「\(1\) 辺とその両端の角がそれぞれ等しい」でした。
相似条件では「\(2\) 組の角がそれぞれ等しい」となります。
相似においては、三角形の大きさはどうでもよく、形が同じかどうかだけが問題となっています。
合同条件において必要だった \(1\) 辺は、倍率何倍で縮小(拡大)してもよいため、もはや長さがどうでもよくなっています。
また、「\(2\) 組の角がそれぞれ等しい」とは、残りの \(1\) つの角も必然的に等しくなるため、三角形の \(3\) つの角がそれぞれ等しいということと同じです。\(3\) つの角が等しければ・・・相似(形が同じ)なのはもはや当たり前のことではないでしょうか。