円と三角形
三角形の内角が、円周角になっている図形配置は非常によく出題されます。
このとき、\(2\) つの三角形の相似を証明するために用いる相似条件は
ほぼ間違いなく
「\(2\) 組の角がそれぞれ等しい」
です。
例題1
下の図で、\(\triangle AED \backsim \triangle BEC\) を証明しなさい。
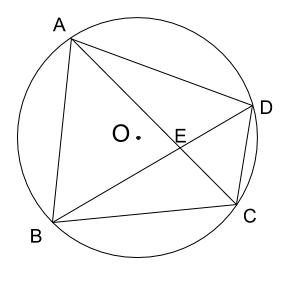
解説
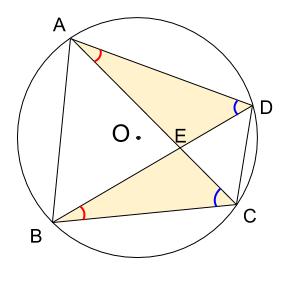
同じ弧に対する円周角は等しいので、
下の図で同じ色をつけた角の大きさは等しいです。
青い角は \(\stackrel{ \Large \frown }{ AB }\) に対する円周角
赤い角は \(\stackrel{ \Large \frown }{ CD }\) に対する円周角
よって、\(2\) 組の角がそれぞれ等しいので \(\triangle AED \backsim \triangle BEC\)
※もちろん、 \(\triangle ABE \backsim \triangle DCE\) も成り立っています。
これを解答にまとめます。
解答
\(\triangle AED\) と \(\triangle BEC\) において
\(\stackrel{ \Large \frown }{ AB }\) に対する円周角だから、\(\angle EDA=\angle ECB\)・・・①
\(\stackrel{ \Large \frown }{ CD }\) に対する円周角だから、\(\angle DAE=\angle CBE\)・・・②
①、②より、\(2\) 組の角がそれぞれ等しいので
\(\triangle AED \backsim \triangle BEC\)
例題2
下の図で、\(\triangle ACE \backsim \triangle BDE\) を証明しなさい。
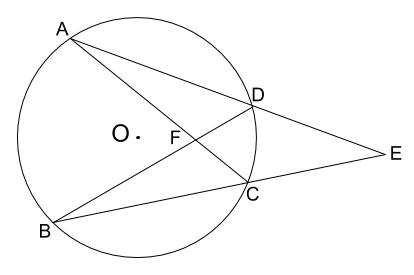
解説
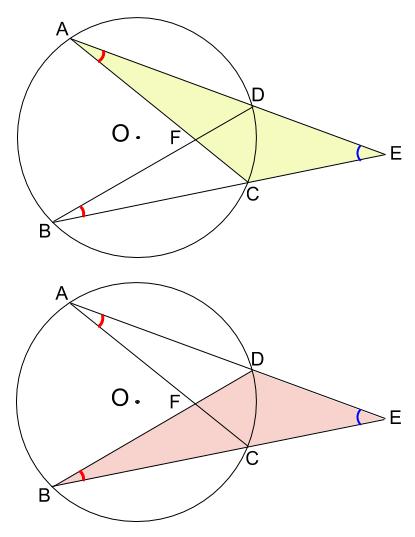
同じ弧に対する円周角は等しいので、同じ色をつけた角の大きさは等しいです。
赤い角は \(\stackrel{ \Large \frown }{ CD }\) に対する円周角
また、青い角は \(2\) つの三角形に共通です。
よって、\(2\) 組の角それぞれが等しいので \(\triangle ACE \backsim \triangle BDE\)
これを解答にまとめます。
解答
\(\triangle ACE\) と \(\triangle BDE\) において
\(\stackrel{ \Large \frown }{ CD }\) に対する円周角だから、\(\angle EAC=\angle EBD\)・・・①
共通なので、\(\angle CEA=\angle DEB\)・・・②
①、②より、\(2\) 組の角がそれぞれ等しいので
\(\triangle ACE \backsim \triangle BDE\)
