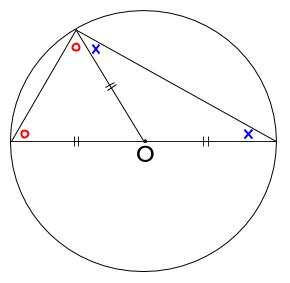
円周角が中心角の半分であることの説明
直線POが弧ABと交わるとき
なぜ円周角は中心角の半分なのでしょうか。
下の図で説明をします。
\(PO\) を通る直線を補助線としてひきます。
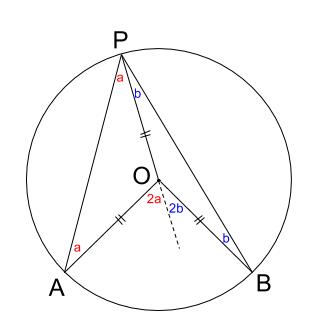
円 \(O\) の半径はすべて等しい長さなので、
二等辺三角形 \(OPA\) と二等辺三角形 \(OBP\) ができます。
これらの内角と外角に着目しましょう。
中心角 \(\angle AOB\)\(=2a+2b\)
円周角 \(\angle APB\)\(=a+b\)
で、等しい弧に対する円周角は中心角の半分であることがわかります。
また点 \(P\) が例の図と異なる位置にあっても、同様の図で円周角が中心角の半分であることが説明できます。
つまり、同じ弧に対する円周角が等しいこともこの考え方で説明ができます。
直線POが弧ABと交わらないとき
点 \(P\) が上の図の位置と大きく異なるときは、上の補助線の説明が不可能になります。
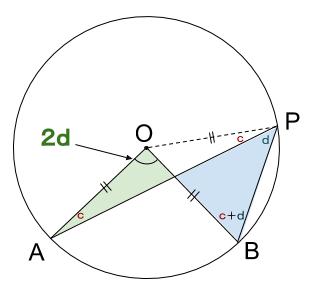
下図のように、直線 \(PO\) が弧 \(AB\) と交わらないときも、円周角が中心角の半分となることは成り立つのでしょうか?
もちろん成り立ちます。
以下のように説明ができます。
直線 \(OP\) をひいて、二等辺三角形 \(OAP\) をつくり、その内角に注目します。
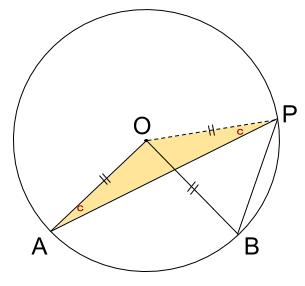
次に、二等辺三角形 \(OBP\) の内角に注目します。
ここで、弧 \(AB\) の円周角の大きさを \(d\) とおきました。
つまり、弧 \(AB\) の中心角の大きさが \(2d\) となることを示すことが最終目標です。
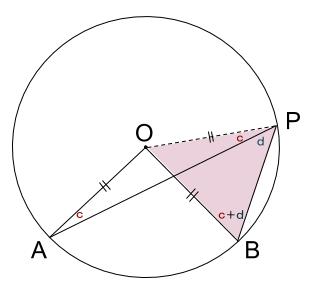
最後にうす緑色の三角形とうす青色の三角形の内角に注目します。対頂角は等しいので、\(\angle AOB=2d\) がわかります。
これで円周角の \(2\) 倍が中心角であることがやはり成り立つことがわかります。
半円の弧の円周角は90°(直角
では、半円の弧の円周角が \(90°\) になることも確認しておきましょう。
今ままでと同様の説明になります。
円に対して行うことのできる図形的操作は、中心から補助線を引くことくらいです。
すると二等辺三角形ができますので。
下図より、半円の弧の円周角は \(90°\) ですね。