例題1
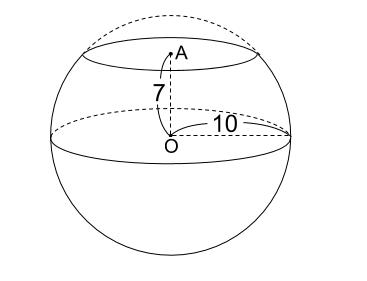
半径 \(10cm\) の球を切り口が円になるように切断しました。
切断面の円の中心 \(A\) と球の中心 \(O\) の距離が \(7cm\) のとき、
切断面の面積を求めなさい。
解答
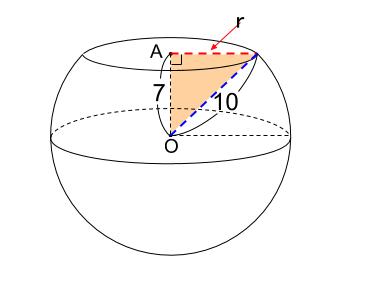
当然ですが、切断面の円の半径が知りたいわけです。
ですからそれを図に入れます。
切断面の円の半径を \(rcm\) とします。
球の半径は \(10cm\) なので、
下の図のクリーム色の直角三角形に三平方の定理を用いれば
切断面の円の半径 \(r\) が求まります。
\(r^2+7^2=10^2\)
\(r^2=100-49\)
\(r^2=51\)
このまま進めて \(r\) を求めてもよいのですが、
この問題で聞かれているのは切断面の面積です。
切断面の面積は
\(r^2×\pi\)
\(=51\pi\)
例題2
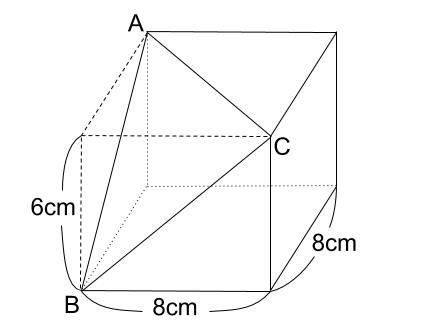
下の図のように、直方体を \(3\) 点 \(A,B,C\) を通る平面で切断しました。
切断面の面積を求めなさい。
解答
下図、オレンジ色の直角三角形に三平方の定理を用いれば
\(BC=10cm\) が得られます。
もちろん、\(3\) 辺の辺の比が \(3:4:5\) の有名直角三角形なので、
それから求めても構いません。
緑色の直角三角形に三平方の定理を用いれば
\(AC=8\sqrt{2}cm\) が得られます。
もちろん、\(3\) 辺の辺の比が \(1:1:\sqrt{2}\) の直角二等辺三角形なので、
それから求めても構いません。
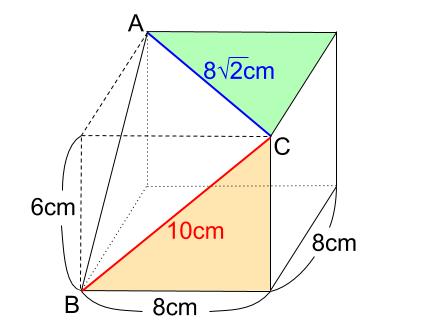
さて、切断面である、三角形 \(BCA\) に注目します。
これは \(BA=BC\) の二等辺三角形です。
図形の対称性から明らかでしょう。
※もちろん \(BA=10cm\) を改めて三平方の定理で求めても構いませんが。
頂点 \(B\) から辺 \(AC\) に垂線を引き、交点を \(H\) とします。
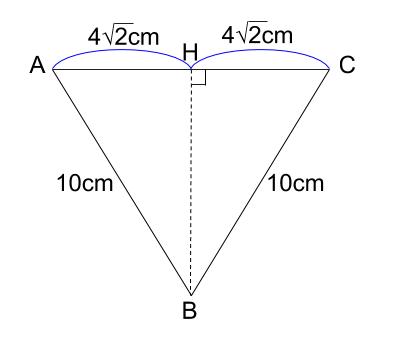
直角三角形 \(ABH\) に三平方の定理を用います。
\(BH^2+(4\sqrt{2})^2=10^2\)
\(BH^2+32=100\)
\(BH^2=68\)
\(BH \gt 0\) なので
\(BH=\sqrt{68}\)
\(BH=2\sqrt{17}\)
よって、切断面である二等辺三角形 \(BCA\) の面積は、
\(8\sqrt{2}×2\sqrt{17}×\displaystyle \frac{1}{2}\)
\(=8\sqrt{34}\)
