例題1
下の図の、\(x\) の値を求めなさい。

解答
下の図のように補助線をひき、左の直角三角形に
三平方の定理を用います。

\(x^2=2^2+8^2\)
\(x^2=68\)
\(x=±\sqrt{68}\)
\(=±2\sqrt{17}\)
この問題では、当然 \(x\) は正の値なので
\(x=2\sqrt{17}\)
例題2
下の図の、\(x\) の値を求めなさい。
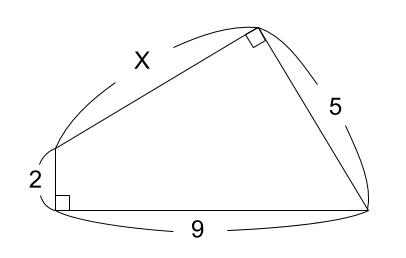
解答
下の図のように補助線をひくと、\(2\) つの直角三角形に割れます。
まずは、左下のピンクの直角三角形に三平方の定理を用います。
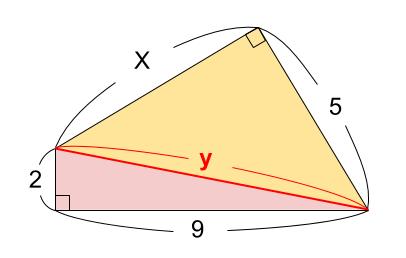
\(y^2=2^2+9^2\)
\(y^2=85\)
この \(y^2\) の値は、右上の直角三角形に三平方の定理を用いたときに
そのまま使えます。
\(y^2=x^2+5^2\)
\(85=x^2+25\)
\(x^2=60\)
\(x=±\sqrt{60}\)
\(=±2\sqrt{15}\)
この問題では、当然 \(x\) は正の値なので
\(x=2\sqrt{15}\)
例題3
下の図の、\(x\) の値を求めなさい。
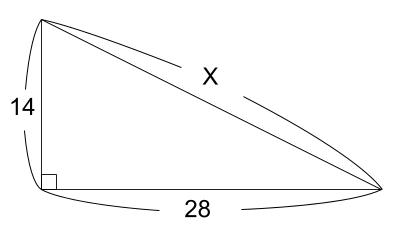
解答
三平方の定理を用いるだけですね。
\(x^2=14^2+28^2\)
あとはこれをひたすら計算すれば答えが出るのですが
\(14^2=196\)
\(28^2=784\)
などの計算はやや面倒です。
\(28=2×14\)
であることを用いて、計算の工夫をしましょう。
\(x^2=14^2+28^2\)
\(x^2=14^2+(2×14)^2\)
\(x^2=14^2+4×14^2\)
\(x^2=14^2×(1+4)\)
\(x^2=14^2×5\)
よって、
\(x=±14\sqrt{5}\)
この問題では、当然 \(x\) は正の値なので
\(x=14\sqrt{5}\)
別解
\(14:28=1:2\)
なので、相似な三角形に対して三平方の定理を用います。
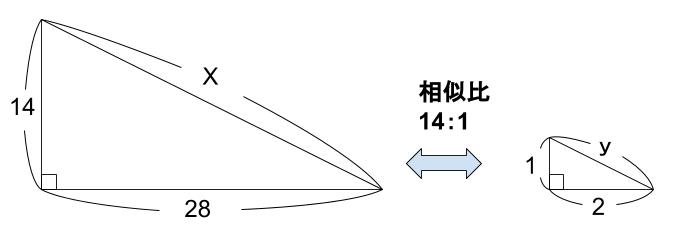
右の小直角三角形に三平方の定理を用います。
\(y^2=1^2+2^2\)
この問題では、当然 \(y\) は正の値なので
\(y=\sqrt{5}\)
相似比は \(14:1\) なので
\(x=14y=14\sqrt{5}\)
