円すいの表面の最短距離
立体の表面を結ぶ線分を考えるとき、展開図をかいて考えます。
重要な解法テクニックであり、必ず暗記しておきましょう。
例題1
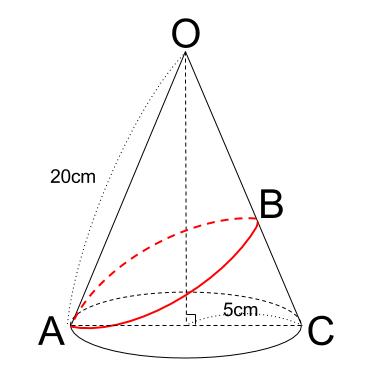
下の図のように、底面の直径が \(10cm\) で、母線の長さが \(20cm\) の円すいに、底面の点 \(A\) から側面を通って \(1\) 周糸をまきつけた。糸の長さが最も短くなるとき、 \(OC\) 上の点 \(B\) を通った。このとき、糸の長さを求めなさい。また、\(OB\) の長さを求めなさい。
解答
円すいの展開図をかきます。
糸の通過している面のみをかけばよいので、
底面の円をかく必要はありません。側面のみかきましょう。
側面はおうぎ形で、その中心角は
\(360×\displaystyle \frac{5}{20}=90°\)
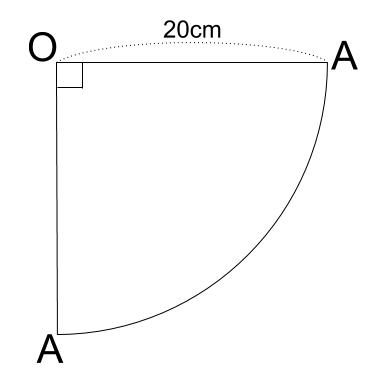
よって、下図のようになります。
\(OA\) で切り開いた展開図です。
組み立てたら一致する場所は同じ点です。
点 \(A\) が \(2\) 箇所あるのはそういうことです。
糸の長さ
\(A\) から \(A\) までを結ぶ最短距離は、一直線です。
よって、まきつけた糸は下図のようになっています。
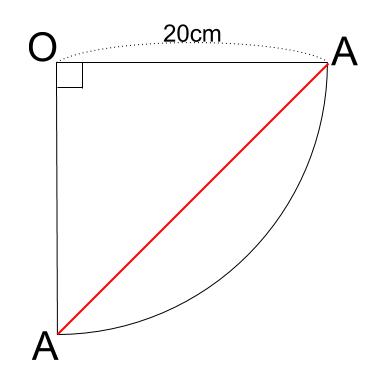
よって、直角二等辺三角形の斜辺の長さが求める糸の長さなので、
\(20× \sqrt{2}=20\sqrt{2}cm\)
\(OB\) の長さ
母線 \(OC\) は、点 \(A\) と反対の位置にあります。
言いかえると、底面の円をぐるり一周すると \(A\) にもどるのですが、そのちょうど半分の地点が点 \(C\) です。
つまり、中間地点なのです。
よって、 \(C,B\) は下図の位置にあります。

三角形 \(OAB\) も直角二等辺三角形なので、\(OB\) の長さは、先ほど求めた糸の長さの半分です。
よって、
\(20\sqrt{2}×\displaystyle \frac{1}{2}=10\sqrt{2}cm\)
以上、求まりました。
