三平方の定理
三平方の定理
直角三角形の \(3\) 辺の長さには、以下のようの関係式が常に成り立ちます。
\(a^2 + b^2 = c^2\)
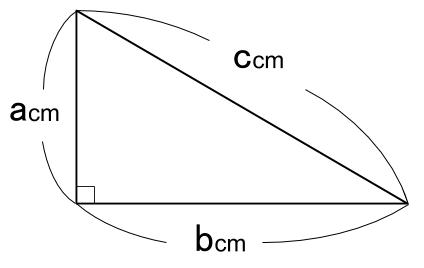
※直角三角形の \(3\) 辺で、最も長い辺は直角の向かいの辺で、この辺を斜辺といいます。
上の三角形の斜辺は、長さが \(Ccm\) の辺です。
なんでこの関係は成り立つの?
という好奇心はちょっと保留して、まずは計算練習をしておきましょう。
例題1
下図の \(x\) を求めなさい。
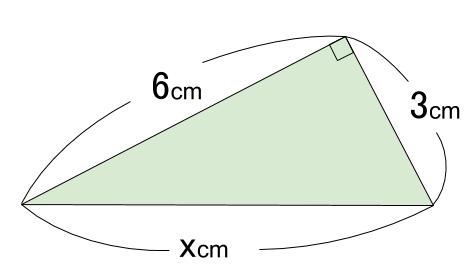
解答
最も長い辺(斜辺)は直角の向かい側であり、この問題では \(X\)\(cm\) の辺が斜辺です。
よって、
\(x^2=3^2 + 6^2\)
\(x^2=9+36\)
\(x^2=45\)
\(x>0\) であるから
\(x=\sqrt{45}\)
\(x=3\sqrt{5}\)
例題2
下図の \(x\) を求めなさい。
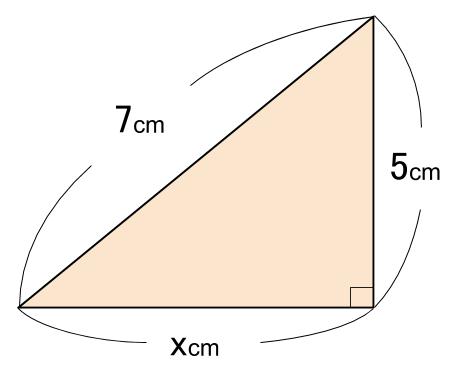
解答
\(x^2 + 5^2 = 7^2\)
\(x^2 + 25= 49\)
\(x^2 =24\)
\(x>0\) であるから
\(x=\sqrt{24}\)
\(x=2\sqrt{6}\)
三平方の定理の逆
\(3\) 辺の長さが、\(a,b,c\) である三角形において、
\(a^2 + b^2 = c^2\) を満たすとき、その三角形は直角三角形であり、長さ \(c\) の辺が斜辺である。
例題3
次の長さを \(3\) 辺とする三角形は、直角三角形であるか、そうでないか判定せよ。
ア \(1cm\), \(3cm\), \(\sqrt{10}cm\)
イ \(5cm\), \(6cm\), \(5\sqrt{3}cm\)
解答
ア
\(1^2 + 3^2 = \sqrt{10}^2\)
が成り立つので、直角三角形である。
イ
\(5\sqrt{3}\) が最も大きい。
\(5^2 + 6^2 =5\sqrt{3}^2\)
は成り立たないので、直角三角形ではない。
