直角三角形の相似
相似の証明でも取り扱った「直角三角形の相似」です。
このページでは辺の長さや比を求めていきましょう。
相似な直角三角形が現れる図形として、最重要・最頻出のものを扱います!
直角である頂点から斜辺へ垂線をひくと相似になる
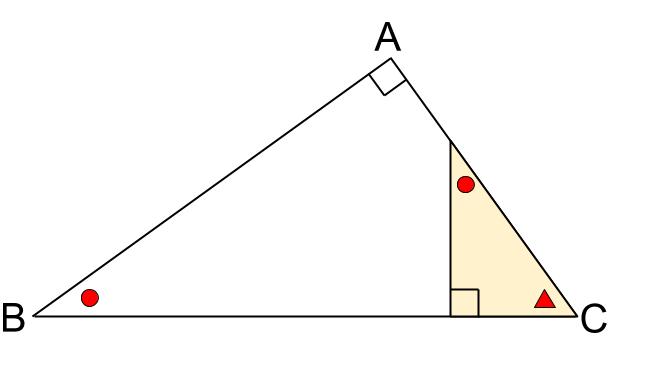
角 \(A\) が直角である直角三角形 \(ABC\) において、点 \(A\) から \(BC\) に垂線を下した図です。
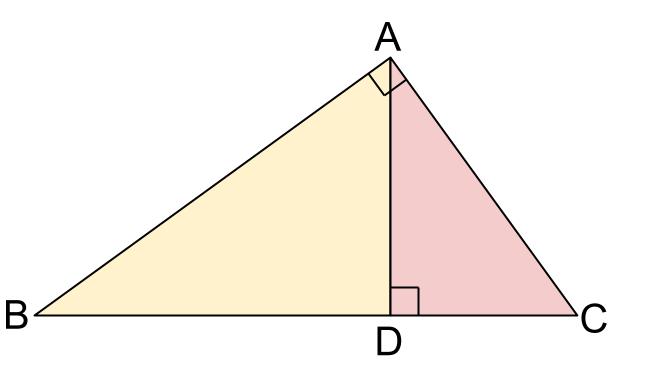
この図の中に、大中小、\(3\) つの直角三角形が見えますね?
大は三角形 \(ABC\)
中は三角形 \(DBA\)
小は三角形 \(DAC\)
すべて相似な直角三角形となります。
相似であることを確かめる
これら \(3\) つの直角三角形が相似であることは、内角の大きさについて考察することで確かめられます。
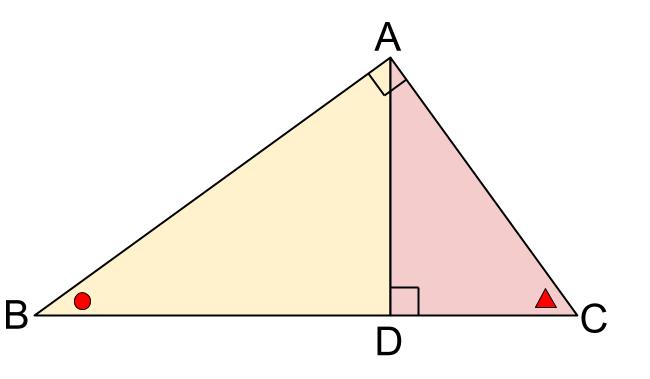
大・中・小、どの直角三角形の内角から着目しても良いのですが、ここでは大三角形 \(ABC\) の内角からはじめます。
下図のように、角 \(ABC\) を丸○、角 \(BCA\) を三角△とします。
※ちなみに、丸○と三角△の和は \(90°\) です。直角三角形ですので。
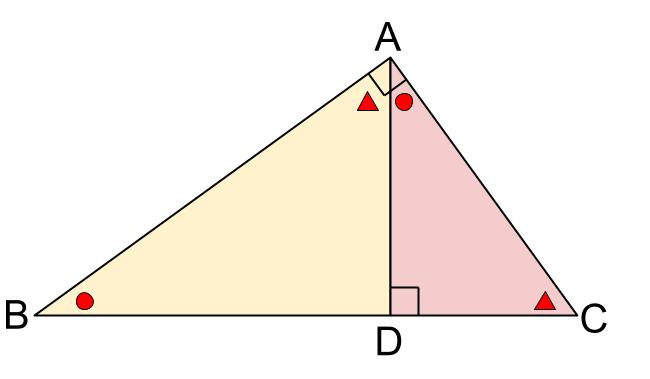
次に、中三角形 \(DBA\) の内角に注目してみます。
直角と丸○なので、大三角形と \(2\) つの角が等しいですね。
これは相似条件を満たします。
大三角形 \(ABC\) と、中三角形 \(DBA\)は相似です。
同様に、小三角形も大三角形と相似であることがわかります。
※三角形において \(2\) つの角が等しいとはつまり、最後の \(1\) つの角も等しいので、
\(3\) つの内角がすべて等しいということです。
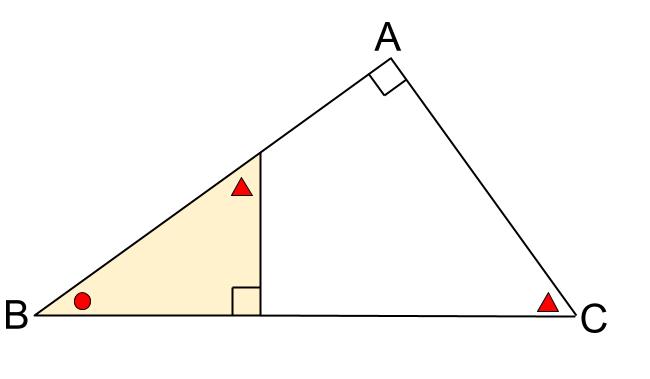
どこでもからでもよいので、斜辺へ垂線をひくと相似
頂点 \(A\) から垂線を下ろさなくとも、相似な直角三角形はできます。
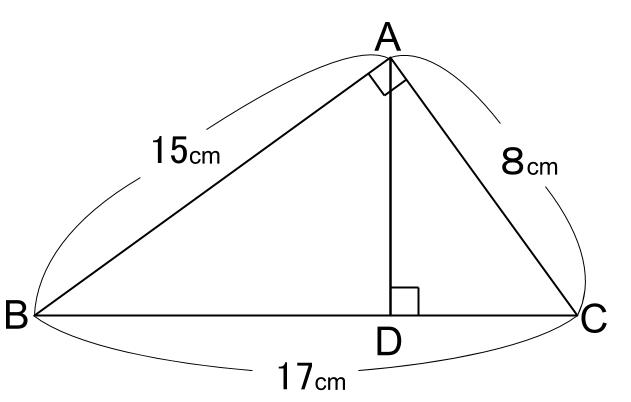
例題1
下の図において、\(AD,BD,DC\) の長さをそれぞれ求めなさい。
解説
大三角形の \(3\) 辺の比が \(8:15:17\) で、中三角形も小三角形も同様です。
中・小どちらの直角三角形に着目しても良いのですが、ここでは中三角形 \(DBA\) に着目しましょう。
\(DB=15×\displaystyle \frac{15}{17}=\displaystyle \frac{225}{17}\)
\(AD=15×\displaystyle \frac{8}{17}=\displaystyle \frac{120}{17}\)
\(CD=BC-DB=17-\displaystyle \frac{225}{17}=\displaystyle \frac{64}{17}\)
以上求まりました。
確認のため、小三角形 \(DAC\) の辺の比から、\(CD\) を求めてみましょう。
\(CD=8×\displaystyle \frac{8}{17}=\displaystyle \frac{64}{17}\)
先の値と一致していますね!
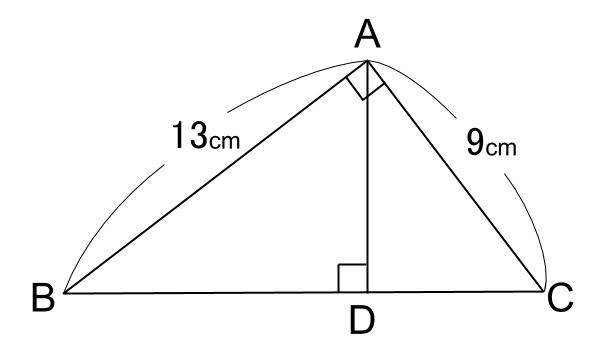
例題2
下図の図において、\(BD\) と \(DC\) の長さの比を求めなさい。
解説
\(BC=5\sqrt{10}cm\) であることは、後ほど習う三平方の定理を適用すれば求められるのですが、この値を使わずとも \(BD\) と \(DC\) の長さの比は求められます。
解き方1
\(BC\) の長さを \(Lcm\) としましょう。
この図形の中にある \(3\) つの直角三角形の辺の長さ比は、いずれも
\(9:13:L\) となります。
中三角形 \(DBA\) に着目すれば、
\(DB=13×\displaystyle \frac{13}{L}=\displaystyle \frac{169}{L}\)
小三角形 \(DAC\) に着目すれば、
\(CD=9×\displaystyle \frac{9}{L}=\displaystyle \frac{81}{L}\)
よって、
\(BD:DC=\displaystyle \frac{169}{L}:\displaystyle \frac{81}{L}=169:81\)
求まりました。
解き方2
直角をはさむ \(2\) 辺の比は、 \(9:13\) なので、
小三角形 \(DAC\) の辺の比は下図のようになっています。
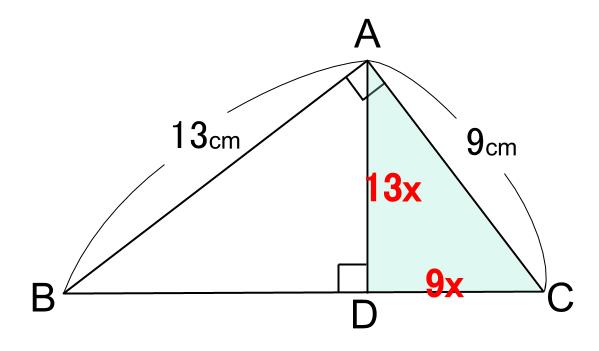
また、中三角形 \(DBA\) の直角をはさむ \(2\) 辺の比も、 \(9:13\) なので、
\(DB=13x×\displaystyle \frac{13}{9}=\displaystyle \frac{169x}{9}\)
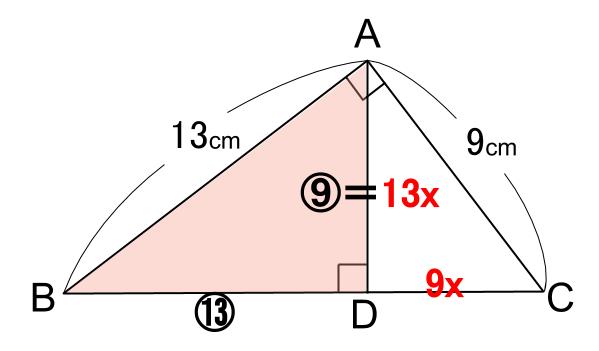
よって、
\(BD:DC=\displaystyle \frac{169x}{9}:9x=169:81\)
求まりました。
参考
相似な三角形の面積比から求めることもできます。
これは三平方の定理の簡潔な証明にもつながる話になります。
気になる人は三平方の定理の証明のページから考えてみてください。
