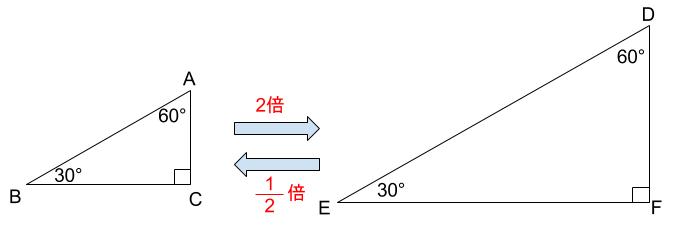
相似とは
ある図形を拡大、縮小した図形は、もとの図形と相似であるといいます。
相似な図形どうしは、まったく同じ形をしているといえます。
例えば下の図の四角形 \(ABCD\) と四角形 \(HEFG\) は相似です。
四角形 \(ABCD \backsim \) 四角形 \(HEFG\)
と表します。
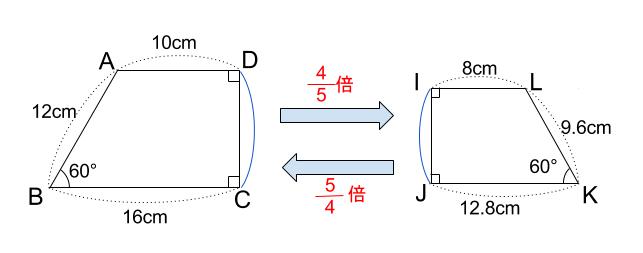
裏返しでも相似
裏返した図形でも相似は成立します。
下の図の四角形 \(LKJI\) も、四角形 \(ABCD\) と相似です。
四角形 \(ABCD \backsim \) 四角形 \(LKJI\)
ここまで、「合同」とほとんど同じような話が続いています。
「合同」とは相似の一種で、拡大(縮小)倍率が \(1\) 倍のものを
「合同」というわけです。
コピー機でコピーをするさい、拡大も縮小もしない、そのまんまが「合同」です。
それ以外、拡大・縮小したものを「相似」というわけです。
相似な図形の対応する頂点、辺、角
合同な図形を、ピッタリ重ねたときに、重なる頂点、辺、角をそれぞれ
対応する頂点
対応する辺
対応する角
といいました。
それと同様に、相似な図形にも、対応する頂点、辺、角 があります。
もし合同になるように拡大したとして・・・
そのときに対応する頂点、辺、角が、
相似な図形の対応する頂点、辺、角です。
感覚的にわかりますね。
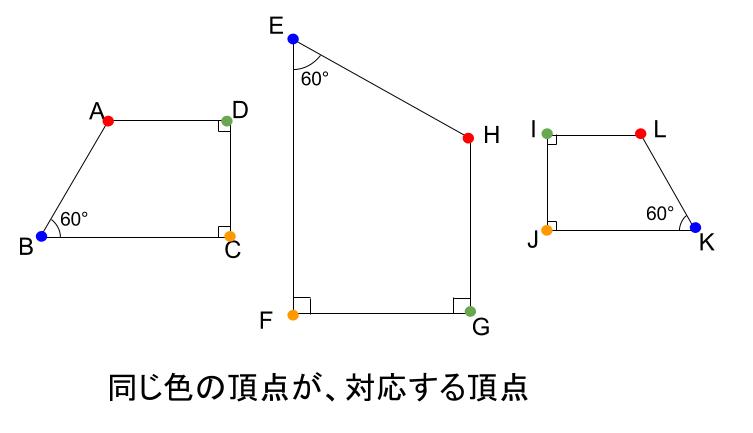
相似な図形は、対応する頂点の順番をそろえて表すことが求められます。
合同のときと同様です。
つまり、
四角形 \(ABCD \backsim \) 四角形 \(HEFG\)
四角形 \(ABCD \backsim\) 四角形 \(LKJI\)
が正しく、
四角形 \(ABCD \backsim \) 四角形 \(EFGH\) とか
四角形 \(ABCD \backsim \) 四角形 \(IJKL\) ではいけません。
安易にアルファベット順に並べればよいわけではないので注意してください。
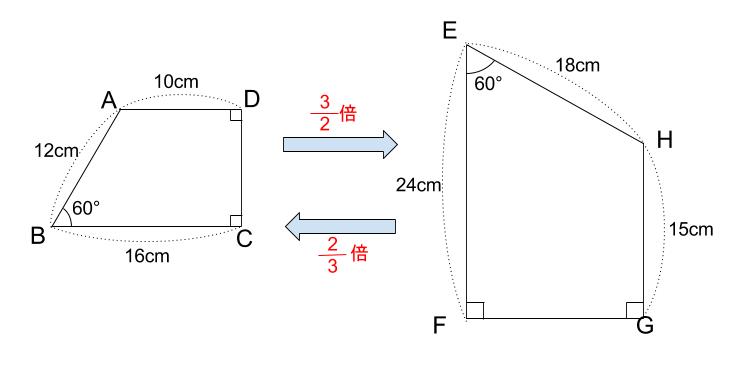
相似な図形の性質
①対応する線分の長さの比は、すべて等しい
倍率 \(\displaystyle \frac{4}{3}\) 倍で拡大したとします。
すると、あらゆる「対応する線分」が \(\displaystyle \frac{4}{3}\) で拡大されます。
下の図で、\(3\) 辺の長さはもちろん、点線部分も \(\displaystyle \frac{4}{3}\) 倍で拡大
されていることに注意しましょう。
対応する線分のすべてが、同じ倍率で拡大・縮小されます。
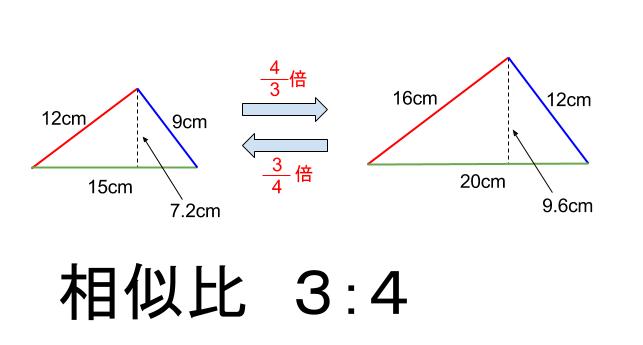
相似な図形があるとき、互いにどれくらい拡大(縮小)した関係にあるのかを
比を用いて表します。
これを相似比といいます。
上の例では、相似比は \(3:4\) です。
②対応する角の大きさはそれぞれ等しい
拡大コピーしても、形は同じです。
\(2\) 倍に拡大しても、角の大きさは \(2\) 倍にはなりません。
角の大きさは拡大・縮小コピーで変化しません。
下の図で、\(\angle ABC=\angle DEF \) です。
合同のとき同様、対応する頂点の順にかきます。
\(\angle ABC=\angle FED\) ではいけません。