【中学数学】2乗に比例の利用・動点・その１

例題１

たてが $10cm$ ,よこが $15cm$ の長方形 $ABCD$ で、点$P$ は点 $B$ を出発して秒速 $2cm$ で辺 $BA$ 上を $A$ まで動き、点 $Q$ は点 $P$ と同時に $B$ を出発して、秒速 $3cm$ で辺 $BC$ 上を $C$ まで動く。$2$ 点 $P,Q$ が同時に $B$ を出発してから $x$ 秒後の三角形 $BPQ$ の面積を $ycm^2$ とする。次の問いに答えなさい。

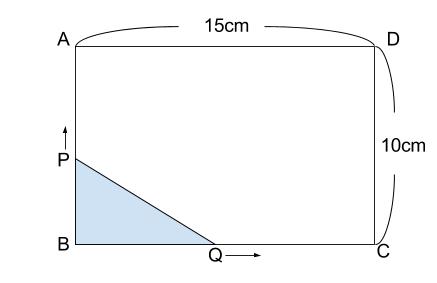
①　$y$ を $x$ の式で表しなさい。
② $x,y$ の変域をそれぞれ求めなさい。
③　$y$ と $x$ の関係を表すグラフをかきなさい。

解説

① $y$ を $x$ の式で表しなさい。

$x$ 秒後の図は以下のようになります。
点$P$ は秒速$2cm$ で $x$ 秒進むので、 $2x(cm)$
点 $Q$ は秒速$3cm$ で $x$ 秒進むので、 $3x(cm)$
それぞれ進んでいます。

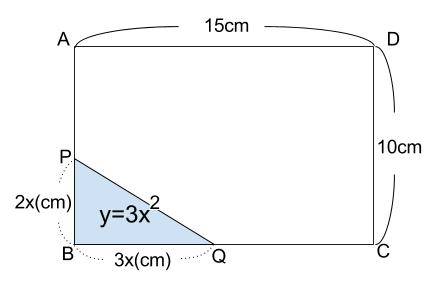
このときの三角形 $BPQ$ の面積 $ycm^2$ は
$y=2x× 3x×\displaystyle \frac{1}{2}=3x^2$
よって、
$y=3x^2$
が求める式になります。

② $x,y$ の変域をそれぞれ求めなさい。

$x$ は $2$ 点 $P,Q$ が出発から、ゴールするまでの間になります。
点$P$ は秒速$2cm$ で進むので $A$ まで動くのに $5$ 秒かかる。
点 $Q$ は秒速$3cm$ で進むので $C$ まで動くのに $5$ 秒かかる。
よって、$x$ の変域は
$0 \leqq x \leqq 5$

$y$ の変域は、①で求めた式に、$x=0$ と $x=5$ を代入して求めます。
$x=0$ のとき、$y=0$
$x=5$ のとき、$y=3×5^2=75$
よって、$y$ の変域は
$0 \leqq y \leqq 75$

※$y$ の変域は、③のグラフをすでに想定しているからこそです。
常に増加し続けるということを暗黙の前提として解いています。

三角形の面積が最大になるのは、$x=5$ のときで下図のようになります。

③ $y$ と $x$ の関係を表すグラフをかきなさい。

①で求めた式、$y=3x^2$ のグラフを
②で求めた変域の範囲でかきます。

スポンサーリンク