例題1
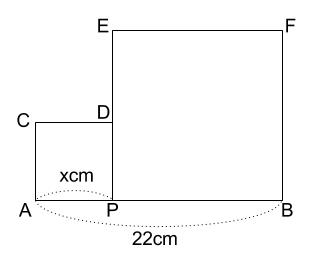
下の図のように、長さ \(22cm\) の線分 \(AB\) 上に点 \(P\) を、\(AP=xcm\) となるようにとり、
正方形 \(CAPD\) と正方形 \(EPBF\) をつくる。この \(2\) つの正方形の面積の和が \(250cm^2\) となるとき、
\(x\) はいくらか求めなさい。
解説
当然ですが、求めたい長さ \(x\) で立式をしましょう。
\(x^2+(22-x)^2=250\)
\(x^2+(22^2-44x+x^2)=250\)
\(2x^2-44x+484=250\)
\(2x^2-44x+234=0\)
\(x^2-22x+117=0\)
\((x-9)(x-13)=0\)
\(x=9,13\)
\(9\) も \(13\) も題意に適する。
よって、\(x=9,13\)
答えは適している?
問題の図をみて、\(x\) は \(AB\) の半分より小さいから、\(13\) は不適!
と思ってしまいましたか?
そんことはありませんよ。
\(9\) と \(13\) 、対称になっています。どちらも答えとして適しています。
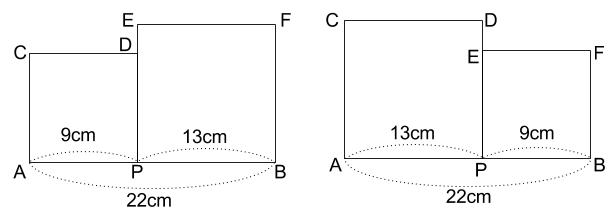
答えは予想できる・・・
ちなみに・・・
この問題の答えは、「整数」であると予想できますね。
だから、平方数を調べていけばみつかりますね。
\(1^2=1\) と \(21^2=441\) これらの和は \(442\)
\(2^2=4\) と \(20^2=400\) これらの和は \(404\)
大きすぎるからもう少し飛ばして調べると
\(10^2=100\) と \(12^2=144\) これらの和は \(244\)
和が \(250\) より小さくなってしまった。
\(1\) つ戻してみると
\(9^2=81\) と \(13^2=169\)
和は \(81+169=250\)
より、見つかりましたね。
もちろん、\(2\) 次方程式をたてて、それを解く練習をすることに意義があるわけですが、
ただし、「調べれば見つかりそうだな」ということがわかることも、数学の能力としては十分必要であり、能力が高いともいえるのです。
例題2
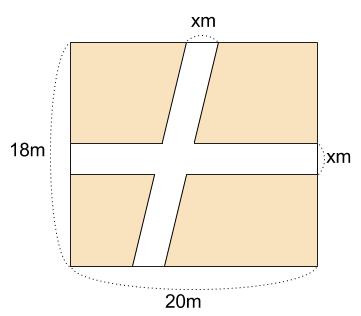
下の図のように、たて \(18m\)、よこ\(20m\) の長方形の土地に、一定の幅 \(xm\) の道をたてよこに \(1\) 本ずつつくる。
残った土地の面積が \(288m^2\) になるには、道の幅を何 \(m\) にすればよいか求めなさい。
解説
道を端によせても、道や残った土地の面積は変わりません。
\(4\) つの土地を一か所に集めるという見方をしても同じです。
有名解法です。
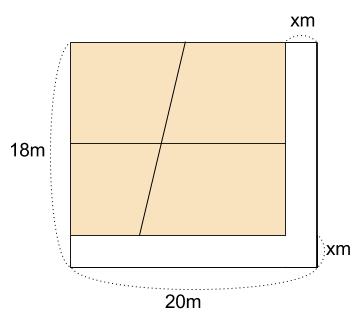
よって、土地の面積は長方形の面積として求めることができます。
\((18-x)(20-x)=288\)
\(x^2-38x+360=288\)
\(x^2-38x+72=0\)
\((x-2)(x-36)=0\)
\(x=2,36\)
\(36\) は、この問題に適さない。
よって、道の幅は\(2m\) とすればよい。
例題3
下の図の斜線部分の面積 \(S\) を \(a\) を用いて表しなさい。
また、\(S=38\) となるような \(a\) はいくらか求めなさい。
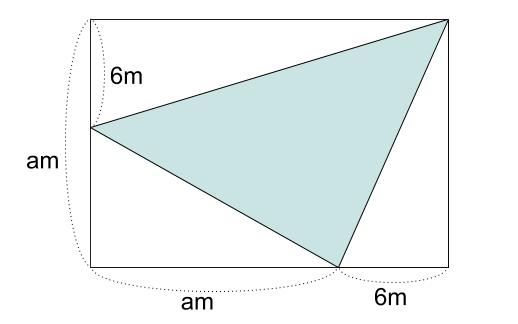
解説
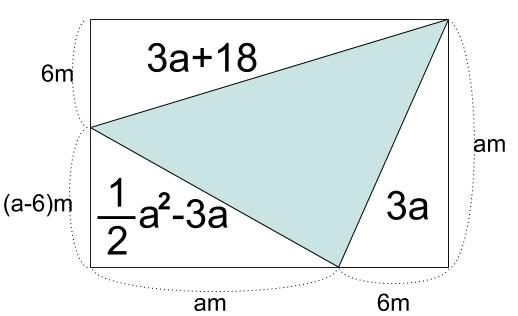
長方形全体から、\(3\) つの直角三角形を引いて、\(S\) を \(a\) の式で表します。
長方形
\(a(a+6)\)
左上の三角形
\(6(a+6)×\displaystyle \frac{1}{2}=3a+18\)
左下の三角形
\(a(a-6)×\displaystyle \frac{1}{2}=\displaystyle \frac{1}{2}a^2-3a\)
右下の三角形
\(6a×\displaystyle \frac{1}{2}=3a\)
斜線の三角形の面積 \(S\)
よって斜線部の三角形の面積 \(S\) は
\(S=a(a+6)-\{(3a+18)+(\displaystyle \frac{1}{2}a^2-3a)+3a\}\)
整理すると
\(S=\displaystyle \frac{1}{2}a^2+3a-18\)
次に、\(S=38\) となるような \(a\) を求めます。
\(\displaystyle \frac{1}{2}a^2+3a-18=38\)
\(\displaystyle \frac{1}{2}a^2+3a-56=0\)
\(a^2+6a-56×2=0\)
なぜ、定数項を \(56×2\) として、いるのか。
もちろん、 \(56×2=112\) なのですが、この計算をすることに意味はないからです。
なぜなら、これから \(2\) 次方程式を解くために因数分解を試みます。
そのとき、\(112=A×B\) となる \(2\) つの整数 \(A,B\) を探します。
\(56×2\) のように、すでに分解されているものを使ったほうが、\(A,B\) を
見つけやすいですね。
今回は、\(112=8×14\) を使用します。
\(a^2+6a-56×2=0\)
\((a-8)(a+14)=0\)
\(a=-14,8\)
\(-14\) は題意に適しません。
よって、\(a=8\)
スポンサーリンク
