【中学数学】平方根の大小・簡略化の逆操作

数直線・平方根の大小関係

根号のついた数の大小関係は、以前にも学習したとおりです。

$a \lt b$ のとき、
$\sqrt{a} \lt \sqrt{b}$
$-\sqrt{b} \lt -\sqrt{a}$

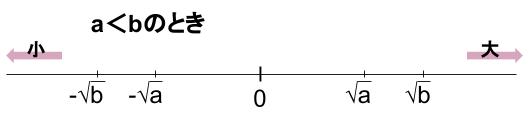
このように、平方根の中の数値の大小を比べることで、
根号のついた数の大小がわかります。
$2\sqrt{3}=\sqrt{3×2^2}=\sqrt{12}$
のように、平方根の簡略化と逆の操作をすることになります。

例題１

次の数の大小を不等号を使って表しなさい。
(1)$3\sqrt{2},2\sqrt{5}$

(2)$-4\sqrt{3},-5\sqrt{2}$

(3)$\sqrt{26},5,2\sqrt{6}$

(4)$\sqrt{\displaystyle \frac{2}{3}},\displaystyle \frac{2}{\sqrt{3}},\displaystyle \frac{\sqrt{2}}{3}$

解説

普通は、平方根の簡略として、
√の中の数を小さくするような操作をします。

しかし、その逆の操作をすることが便利なときもあります。
$\sqrt{a} \lt \sqrt{b}$
のように大小を比べたいときです。

$c\sqrt{d}=\sqrt{d×c^2}$

これを利用します。

(1)$3\sqrt{2},2\sqrt{5}$

$3\sqrt{2}=\sqrt{2×3^2}=\sqrt{18}$
$2\sqrt{5}=\sqrt{5×2^2}=\sqrt{20}$
つまり、
$\sqrt{18} \lt \sqrt{20}$ なので
$3\sqrt{2} \lt 2\sqrt{5}$

(2)$-4\sqrt{3},-5\sqrt{2}$

$-4\sqrt{3}=-\sqrt{3×4^2}=-\sqrt{48}$
$-5\sqrt{2}=-\sqrt{2×5^2}=-\sqrt{50}$
つまり、
$-\sqrt{50} \lt -\sqrt{48}$ なので
$-5\sqrt{2} \lt -4\sqrt{3}$

(3)$\sqrt{26},5,2\sqrt{6}$

$5=\sqrt{5^2}=\sqrt{25}$
$2\sqrt{6}=\sqrt{6×2^2}=\sqrt{24}$
つまり、
$\sqrt{24} \lt \sqrt{25} \lt \sqrt{26}$ なので
$2\sqrt{6} \lt 5 \lt \sqrt{26}$

(4)$\sqrt{\displaystyle \frac{2}{3}},\displaystyle \frac{2}{\sqrt{3}},\displaystyle \frac{\sqrt{2}}{3}$

分母を有理化して、分子での大小比較をしましょう。
$\sqrt{\displaystyle \frac{2}{3}}$

$=\displaystyle \frac{\sqrt{2}}{\sqrt{3}}$

$=\displaystyle \frac{\sqrt{2×3}}{\sqrt{3×3}}$

$=\displaystyle \frac{\sqrt{6}}{3}$

$\displaystyle \frac{2}{\sqrt{3}}$
$=\displaystyle \frac{2×\sqrt{3}}{\sqrt{3}×\sqrt{3}}$
$=\displaystyle \frac{\sqrt{3×2^2}}{3}$
$=\displaystyle \frac{\sqrt{12}}{3}$

$3$ つの数の分子の大小関係、$2 \lt 6 \lt 12$ より、
$\displaystyle \frac{\sqrt{2}}{3} \lt \displaystyle \frac{\sqrt{6}}{3} \lt \displaystyle \frac{\sqrt{12}}{3}$　なので

$\displaystyle \frac{\sqrt{2}}{3} \lt \sqrt{\displaystyle \frac{2}{3}} \lt \displaystyle \frac{2}{\sqrt{3}}$

例題２

次の条件にあてはまる整数を求めなさい。
$\sqrt{30}$ より大きく、$\sqrt{90}$ より小さい整数をすべて求めなさい。

解説

整数 $A$ は　$A=\sqrt{A^2}$ と表されることを用います。

つまり、$30$ より大きく $90$ より小さい平方数を探します。

この条件にあう平方数は、$36,49,64,81$ があります。
つまり、
$\sqrt{30} \lt \sqrt{36}=6 \lt \sqrt{90}$
$\sqrt{30} \lt \sqrt{49}=7 \lt \sqrt{90}$
$\sqrt{30} \lt \sqrt{64}=8 \lt \sqrt{90}$
$\sqrt{30} \lt \sqrt{81}=9 \lt \sqrt{90}$

よって
求める整数は、$6,7,8,9$ となります。

スポンサーリンク

次のページ $\sqrt{n}$ が整数となるような $n$

前のページ 平方根の値の簡略化