例題1
下の図のように、半径 \(rm\) の円形の土地の周りに、幅 \(am\) の道がある。この道の面積を \(Sm^2\) 、道の中央を通る線の長さを \(Lm\) とすると、\(S=aL(m^2)\) となることを説明しなさい。
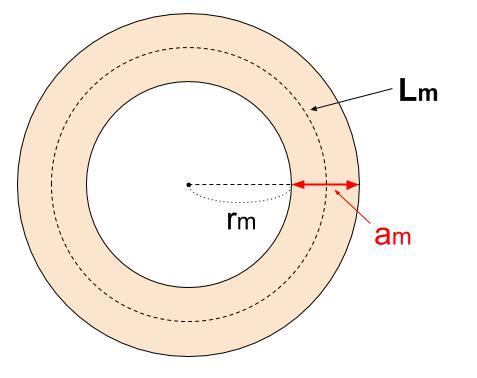
解説
どうやって説明ができるのか、初見では見当もつかないのが当然です。
解説を読んで、慣れていきましょう。
結論からいうと、この問題では「文字が多すぎる」のです。
\(r,a,S,L\) の \(4\) つが与えられていますが、
こんなにいらないでしょって話です。
\(r,a\) の \(2\) つがあれば、\(L\) や \(S\) を表せます。
半径が決まれば、周や面積を求めることができますからね。
つまり、
\(L=rとaの式\)
\(S=rとaの式\)
と表すのです。
あとは、\(2\) つの式を見比べれば結論に至ることができるでしょう。
つまり、\(S=aL(m^2)\) が目指すべき等式ですが、
式をいじくってみて、初めてこの等式の成立がわかるのです。
解答
道の面積 \(S\) は、大円から小円を引くことで求められます。
\(S=(r+a)^2\pi-r^2\pi\)
\(=2ar\pi+a^2\pi\)
\(=a(2r+a)\pi\)・・・①
また、道の中央を通る線の長さを \(L\) は
\(L=(r+\displaystyle \frac{a}{2})×2×\pi\)
\(=(2r+a)\pi\)・・・②
①、②より
\(S=aL\)
例題2
下の図のように、\(1\) 辺の長さが \(xm\) の正方形の土地の周りに、幅 \(am\) の道がある。道の中央を通る線の長さが \(Lm\) 、道の面積が \(Sm^2\) とすると、 \(S=aL(m^2)\) となることを説明しなさい。

解説
例題1とほぼ同じような問題ですね。
\(x,a\) の \(2\) つで、\(L\) や \(S\) を表すことがでそうです。
つまり、
\(L=xとaの式\)
\(S=xとaの式\)
と表してみましょう。
解答
道の面積 \(S\) は
\(S=(x+2a)^2-x^2\)
\(=x^2+4ax+4a^2-x^2\)
\(=4ax+4a^2\)・・・①
\(L=4(x+a)\)・・・②
①、②より、
\(S=4ax+4a^2\)
\(=4a(x+a)\)
\(=aL\)
よって、示された。
この問題をより深く味わう
もしこの問題が、「\(S\) と \(L\) の間にどのような関係式があるか示せ」だったとしましょう。
もちろん、\(S=aL\) という関係式が答えとなるのですが・・・
!あれれ!\(x\) は関係ないんだ!!
という驚きをもってもらいたいんですよ。
この問題は。
例題1でしたら \(r\) に無関係ということです。
\(x\) や \(r\) は無関係なんです。
つまり、\(x,r\) の値がいくつでもこの関係式は成り立つんです。
ちょっと不思議な感じがしませんか?
いやいや、改めて図を見れば、「あたりまえ」っていう感じもしてきます。
ぜひ、示した等式の図形的意味まで味わってください。
別解
上の例題1,2、で示したように、
「文字式をいじくってみれば、示したい等式に変形をすることができる」
という解法は、誰にでもおススメできる無敵の解法です。
しかし、これ以外の説明はいくらでもあります。
数学は凝り固まった学問ではありません。
例題2の別解を1つ示しておきます。
面積を直接求めてしまえ!
道の面積 \(S\) を求めます。
下図のようのに合同な \(4\) つの台形に分けて考えることができます。
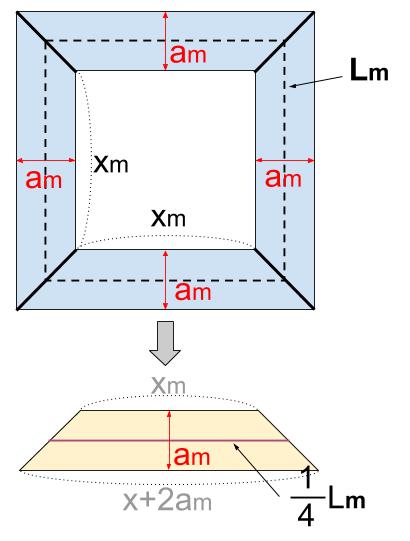
この台形の面積 \(\displaystyle \frac{1}{4}S\) を求めますが、上底も下底も使いません。
下図のような等積変形で、長方形にします。

たて \(am\)
よこ \(\displaystyle \frac{1}{4}Lm\)
の長方形の面積 \(\displaystyle \frac{1}{4}S\)
\(\displaystyle \frac{1}{4}S=\displaystyle \frac{1}{4}L×a\)
よって
\(S=aL\)
が示されました。
この解法ですと、はじめから最後まで \(x\) を使用しませんでした。
\(x\) は無関係なのですから、このような解法も存在します。
スポンサーリンク
