平方の公式
展開の公式があと \(2\) つありました。
それ対応する因数分解が当然 \(2\) つあります。
まずは平方の公式です。
\(x^2+2ax+a^2=(x+a)^2\)
\(x^2-2ax+a^2=(x-a)^2\)
例題1
次の式を因数分解しなさい。
\(x^2+8x+16\)
解説
まずは前回習得した方法で因数分解をしてみましょう。
積が \(+16\) になる数を書き出します。
その中で、和が \(+8\) になるものを探します。
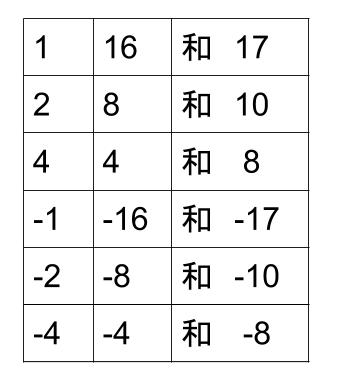
つまり、
\(x^2+8x+16=(x+4)(x+4)=(x+4)^2\)
\(x^2+8x+16=(x+4)^2\)
ということです。
うまく因数分解ができました。
平方の公式の利用
ところで、定数項が平方数であるとき、
この「平方の公式」
\(x^2+2ax+a^2=(x+a)^2\)
\(x^2-2ax+a^2=(x-a)^2\)
が使えるかも!?
と思って欲しいわけです。
今回の式ですと
\(x^2+8x+16\)
定数項の \(16\) は、平方数、\(4^2\) です。
\(x\) の \(1\) 次の項の係数が、この \(4\) の \(2\) 倍になっていれば
平方の公式が適用できます。
今回はこれが適用できます。
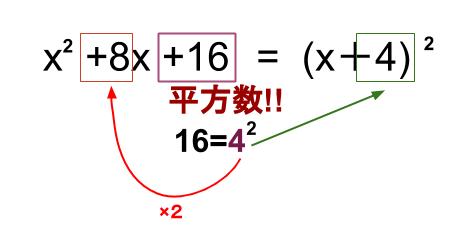
という流れになります。
ですので、はじめに見たように、乗法公式で解いてもらってもまったく問題はありません。
ただ、平方の因数分解になっている!って数の感覚を鍛えておくとより速く因数分解ができます。
例題2
次の式を因数分解しなさい。
\(x^2-12x+36\)
解説
定数項、\(36\) は平方数です。\(36=6^2\)
よって、平方の公式が利用できるか頭をめぐらしましょう。
具体的には、\(6\) の \(2\) 倍の \(12\) が、\(x\) の \(1\) 次の項の係数になっているかどうかの確認です。
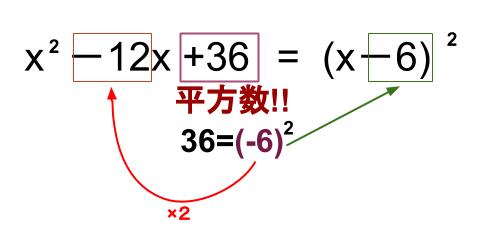
よって、これは平方の公式が成立します。
\(x^2-12x+36=(x-6)^2\)
ちなみに、定数項が平方数でも、平方の公式にならないときもあります。
例
\(x^2+13x+36=(x+4)(x+9)\)
必ず \(x\) の \(1\) 次の項の係数のチェックまで必要です。
和と差の公式
つづいて和と差の展開の逆です。
\(x^2-a^2=(x+a)(x-a)\)
\(x\) の \(1\) 次の項がないときに適用できます。
\(2\) 乗の差は、和と差の積
これは非常に覚えやすく、計算も簡単です。
例題1
次の式を因数分解しなさい。
\(x^2-64\)
解説
「\(2\) 乗の差は、和と差の積」です。
\(x^2-64=(x+8)(x-8)\)
例題2
次の式を因数分解しなさい。
\(9-x^2\)
解説
「\(2\) 乗の差は、和と差の積」です。
\(9-x^2=(3+x)(3-x)\)
この式全体を \(-1\) でくくって
\(9-x^2=(3+x)(3-x)\)
\(=-(x+3)(x-3)\)
とすることもできます。
おまけ
\(2\) 乗の差は、和と差の積、これは \(x\) の \(1\) 次の項がないときに適用できると上で確認しました。
\(x\) の \(1\) 次の項がないということは、言い換えれば、\(x\) の \(1\) 次の項の係数が \(0\) ということです。
つまり、
\(x^2-64=x^2+0x-64\)
なので、
積が \(-64\) で、和が \(0\) になる数を探す!!
という乗法公式の考え方でこの因数分解をすることができます。
\(8\) と \(-8\) の \(2\) つの積が \(-64\)、和が \(0\) なので、
\(x^2-64=(x+8)(x-8)\)
スポンサーリンク
