分配の法則
「単項式と多項式の乗除」
いかついタイトルですが、難しく考えることはありません。
要は、「分配法則」です。
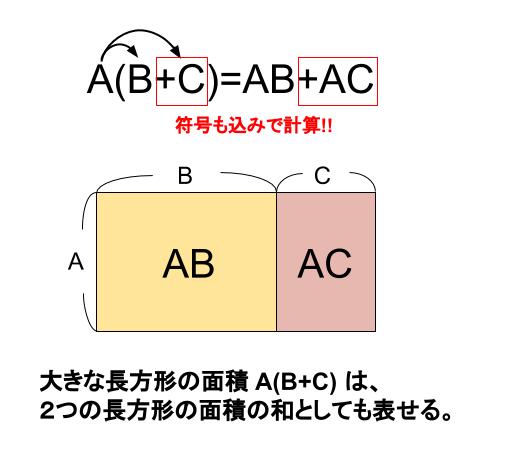
\(A(B+C)=AB+AC\)
のことですね。
このように、かっこをはずす計算をして、単項式の和の形に表すことを
展開する
といいます。
もちろん
\((B+C)A=AB+AC\)
\(A(B+C+D)=AB+AC+AD\)
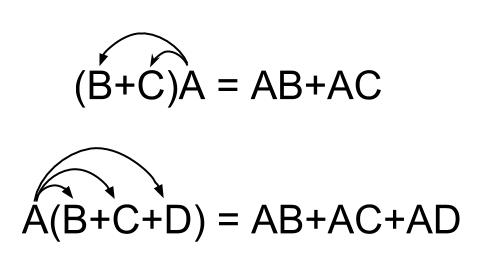
が同様に成り立つことも明らかですね!
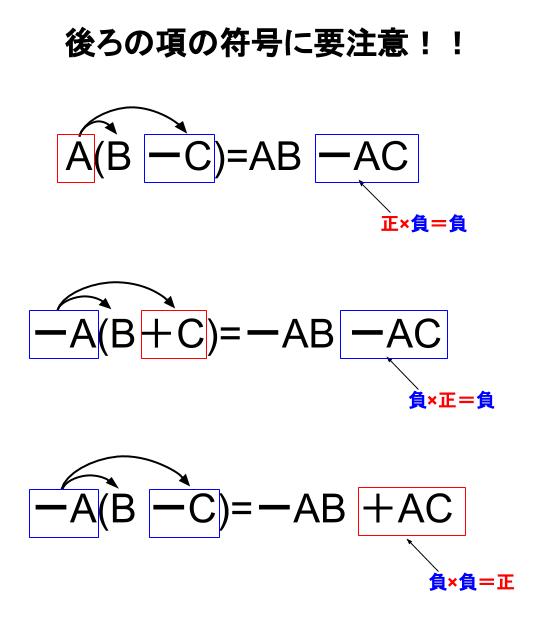
符号についての注意
負の数が入ってきたときの符号には要注意です。
\(A(B-C)=AB-AC\)
\(-A(B+C)=-AB-AC\)
\(-A(B-C)=-AB+AC\)
例題
次の式を展開しなさい。
(1) \(\displaystyle \frac{1}{2}a(a+6)\)
(2) \(3x(5x-4)\)
(3) \(-2x(x+3)\)
(4) \(-\displaystyle \frac{1}{8}(6x-4)\)
(5) \((9x^2-3x)÷(-\displaystyle \frac{3}{2}x)\)
(6) \((x^2-5x+3)×(-x)\)
解答
(1) \(\displaystyle \frac{1}{2}a(a+6)=\displaystyle \frac{1}{2}a^2+3a\)
(2) \(3x(5x-4)=15x^2-12x\)
(3) \(-2x(x+3)=-2x^2-6x\)
(4) \(-\displaystyle \frac{1}{8}(6x-4)=-\displaystyle \frac{3}{4}x+\displaystyle \frac{1}{2}\)
(5) \((9x^2-3x)÷(-\displaystyle \frac{3}{2}x)=(9x^2-3x)×(-\displaystyle \frac{2}{3x})=-6x+2\)
(6) \((x^2-5x+3)×(-x)=-x^3+5x^2-3x\)
スポンサーリンク
