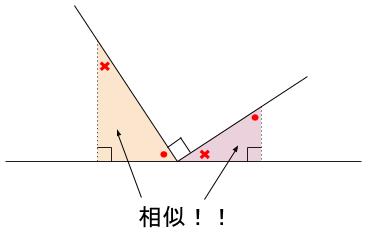
相似の証明・直角三角形型
直角三角形が関わる有名図形配置について学習します。
例題1
下の図のように、直角三角形 \(ABC\) において、点 \(A\) から辺 \(BC\) に向かって垂線をひき、辺 \(BC\) との交点を \(D\) とします。このとき、\(\triangle ABD \backsim \triangle CAD\) を証明しなさい。
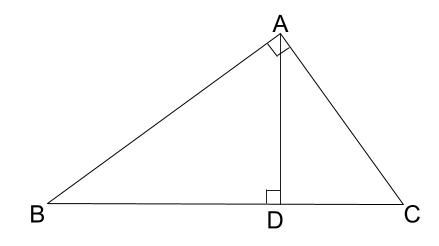
解説
まず、自分自身で \(\triangle ABD \backsim \triangle CAD\) を確認します。
辺の長さに関する情報は一切ないので、
「\(2\) 組の角がそれぞれ等しい」
を用いることになりそうですね。
角に記号を入れていく
角の情報を入れていきます。
直角三角形を扱うときに、用いる常套手段があります。
角に記号を入れていきます。
\(\triangle ABD\) の内角に記号をいれます。
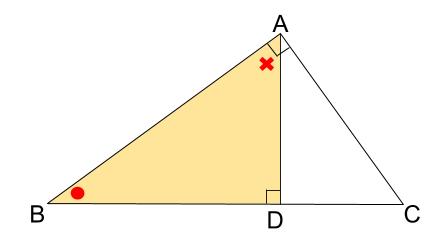
\(○+×=90°\) です。
次に、\(\triangle CAD\) の内角に着目します。
\(\angle CAD=90°-×=○\)
です。
よって、\(\angle DCA=90°-○=×\)
とわかります。
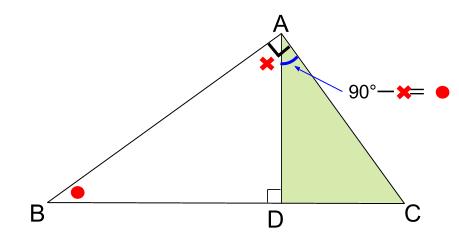
以上より、\(2\) つの角が等しいので相似といえます。
解答
\(\triangle ABD\) と \(\triangle CAD\) において、
仮定より、\(\angle BDA=\angle ADC\)・・・①
三角形 \(ABD\)の内角より、
\(\angle ABD=180°-90°-\angle DAB\)
\(=90°-\angle DAB\)・・・②
\(\angle CAB=90°\) なので、
\(\angle CAD=90°-\angle DAB\)・・・③
②、③より、
\(\angle ABD=\angle CAD\)・・・④
①、④より、\(2\) つの角が等しいので
\(\triangle ABD \backsim \triangle CAD\)
参考
この例題の図には、\(3\) つの直角三角形があります。
そのすべてが相似です。
つまり、上で示した \(\triangle ABD \backsim \triangle CAD\) だけでなく、
\(\triangle ABD \backsim \triangle CAD \backsim \triangle ABC\)
です。
暗記しておくべき重要図形配置です。
例題2
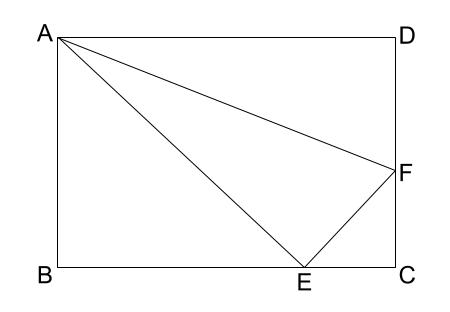
下の図のように、長方形 \(ABCD\) を \(AF\) で折ると、点 \(D\) が辺 \(BC\) に重なります。その位置を点 \(E\) とします。このとき、\(\triangle ABE \backsim \triangle ECF\) を証明しなさい。
解説
例題1と同様の手法で証明します。
下の図のように、角が等しくなっていることがわかります。
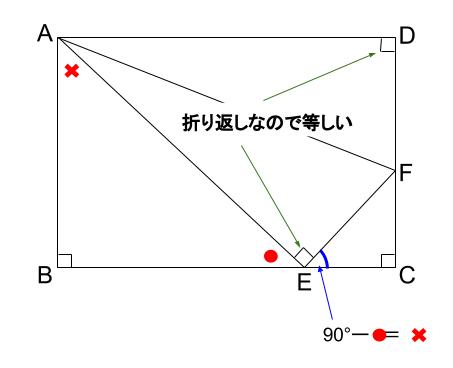
以上より、\(2\) つの角が等しいので相似といえます。
解答
\(\triangle ABE\) と \(\triangle ECF\) において、
仮定より、\(\angle ABE=\angle ECF\)・・・①
三角形 \(ABE\) の内角より、
\(\angle EAB=180°-90°-\angle BEA\)
\(=90°-\angle BEA\)・・・②
折り返しなので、
\(\angle FEA=\angle FDA=90°\)・・・③
頂点 \(E\) に集まる角の和は \(180°\) なので
\(\angle FEC=180°-\angle FEA-\angle BEA\)・・・④
③、④より、
\(\angle FEC=90°-\angle BEA\)・・・⑤
②、⑤より、
\(\angle EAB=\angle FEC\)・・・⑥
①、⑥より、\(2\) つの角が等しいので
\(\triangle ABE \backsim \triangle ECF\)
参考
下の図のように、一直線と直角が組みあわさったとき、相似ができます。
暗記しておくべき重要図形配置です。