三角形の相似の証明
中学2年で学習した、三角形の合同の証明とほぼ同じです。
用いるのが合同条件ではなくて、相似条件になっただけです。
三角形の合同の証明があやふやな人は、そこから学習をしましょう。
急がば回れです。
証明の手順
証明の手順は「合同の証明のときと同様です」
- 結論がなぜいえるのかを「自分自身でわかること」
- それを数学の証明の書式で、清書する
1をもうすこし詳しくみましょう。
相似条件は「辺の比」と「角度」に着目しているので
まずは、図の中に辺の長さや角の大きさの情報を入れていきます。
具体的な長さや大きさが分からなくても、等しいことが分かって入れば同じ印をいれます。
やみくもに入れると図がごちゃごちゃしすぎて、ポイントが掴みづらくなることがあります。
最終目標に関わる箇所から入れていきましょう。
例題1
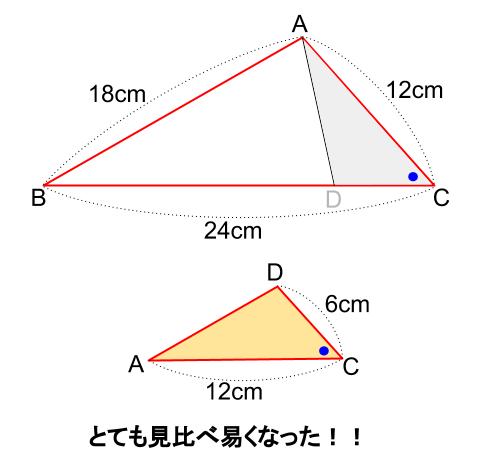
下の図で、\(\triangle ABC \backsim \triangle DAC\) を証明しなさい。
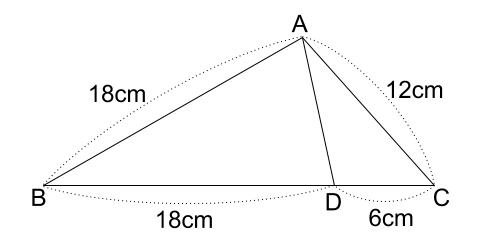
解説
まず、自分自身で \(\triangle ABC \backsim \triangle DAC\) を確認します。
三角形の相似条件のうち、どれを満たしているのかを確認するのです。
よって、「等しい角を探すこと」と「辺の比」を求めることをします。
証明を書く前の準備段階です。
まず、どの三角形が話題の \(2\) つなのか、しっかりと確認します。
下の図の赤い太い三角形\(\triangle ABC\)と、クリーム色の三角形\(\triangle DAC\)です。
青丸の角が、共通なので等しいですね。
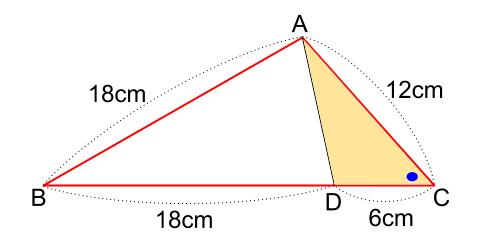
よって、
「あともう \(1\) つ、角の大きさが等しい」
か
「\(2\) 組の辺の比が等しい(ただし、青丸の角をはさむ \(2\) 辺)」
のどちらかをいえばよいのです。
当然ですが、
「三角形の相似条件」を暗記しているからこそ、何を目指せばよいのかがわかるのです。
最終目標から逆算して考えることが大事です。
今回は、辺の長さが様々に与えられています。
「\(2\) 組の辺の比が等しい(ただし、青丸の角をはさむ \(2\) 辺)」
がいえそうです。
実際にいえるかどうか、確認をします。
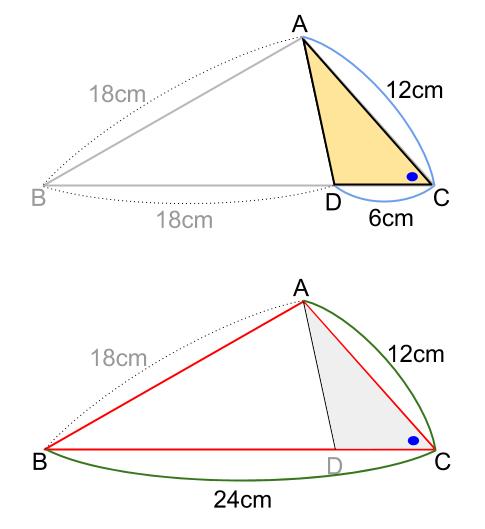
どちらも、青丸の角をはさむ \(2\) 辺の比が \(1:2\) になっています。
よって、「\(2\) 組の辺の比が等しく、その間の角が等しい」ので相似が成り立ちます。
これを解答にまとめます。
解答
\(\triangle ABC\) と \(\triangle DAC\) において、
仮定より、\(AC:DC=12:6=2:1\)・・・①
仮定より、\(BC:AC=24:12=2:1\)・・・②
共通なので、\(\angle BCA=\angle ACD\) ・・・③
①、②、③より、\(2\) 組の辺の比が等しく、その間の角が等しいので
\(\triangle ABC \backsim \triangle DAC\)
2つの三角形の向きをそろえると楽
上の解説はいかがでしたか?
例題1では、相似を示すべき \(2\) つの三角形が重なっていたため、
辺の比の情報が読みとりづらくなっています。
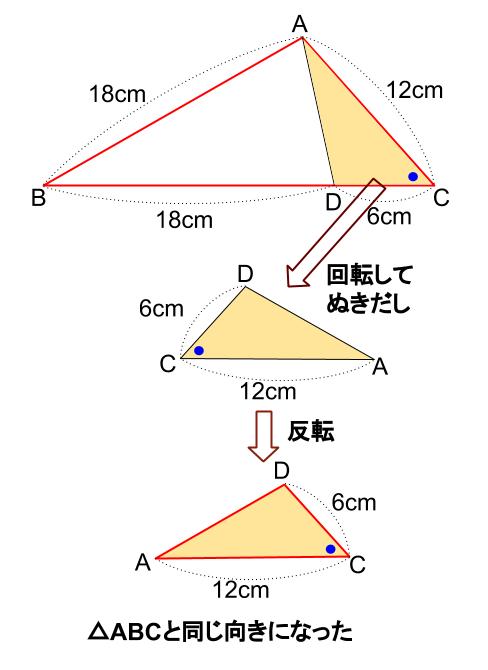
初心者のうちは、
\(2\) つの三角形の向きがそろうように図を自分でかく
という解法も試してみてください。
例題2
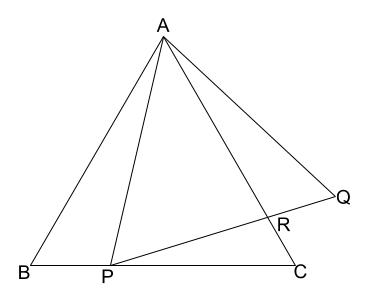
下の図のように、正三角形 \(ABC\) の辺 \(BC\) 上に点 \(P\) をとり、\(AP\) を \(1\) 辺とする正三角形 \(APQ\) をつくる。\(AC\) と \(PQ\) の交点を \(R\) とするとき、\(\triangle ABP \backsim \triangle AQR\) を証明しなさい。
解説
\(\triangle ABP \backsim \triangle AQR\) が最終目標です。
\(2\) つの三角形の辺、角について順に見ていきましょう。
辺の長さの比については、まったく情報がありません。
角は、正三角形の内角と等しい \(60°\) がわかります。
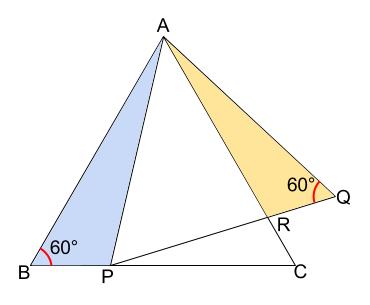
さて、
「もう \(1\) つ等しい角」
か
「 \(60°\) をはさむ \(2\) 組の辺の比が等しい」
のどちらかを示さないといけません。
どちらが示せるか考えてみてください。
ずばり、
「もう \(1\) つ等しい角」
がいえます。
正三角形の内角 \(60°\) を用います。
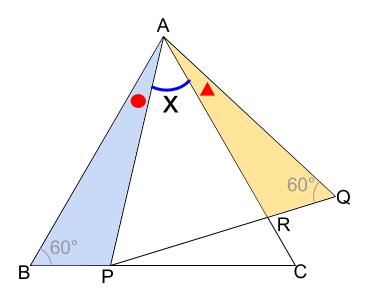
下の図において、
\(○+x=60°\)・・・正三角形 \(ABC\) の内角
\(△+x=60°\)・・・正三角形 \(APQ\) の内角
よって、\(○=△\)
以上より、「\(2\) 組の角が等しい」ので相似です。
これを解答にまとめます。
解答
\(\triangle ABP\) と \(\triangle AQR\) において、
仮定より、正三角形の1つの内角は \(60°\) なので
\(\angle ABP=\angle AQR\)・・・①
仮定より、正三角形の1つの内角は \(60°\) なので
\(\angle PAB+\angle CAP=60°\)・・・②
仮定より、正三角形の1つの内角は \(60°\) なので
\(\angle RAQ+\angle CAP=60°\)・・・③
②、③より、
\(\angle PAB=\angle RAQ\)・・・④
①、④より、\(2\) 組の角が等しいので
\(\triangle ABP \backsim \triangle AQR\)
相似条件の使用頻度
辺の長さが与えられずに相似を証明するときの相似条件は
「\(2\) 組の角がそれぞれ等しい」
であることがほとんどです(全部と言ってしまってよいくらい)。
また相似を証明する問題の大半が、
「\(2\) 組の角がそれぞれ等しい」
を用います。
\(9\) 割近くがこれです。
残り \(1\) 割が
「\(2\) 組の辺の比が等しく、その間の角が等しい」
です。
ほとんど出てこないのが
「\(3\) 組の辺の比が等しい」
です。
頭に入れておいてください。
