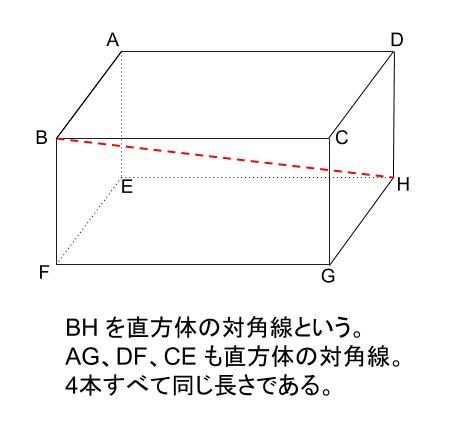
直方体の対角線
立体にも対角線という言葉を用います。
直方体の対角線とは、下図のような
内部を貫く線分のことです。
直方体の対角線の長さ
たて、横、高さがそれぞれ、\(a,b,c\) である直方体の対角線の長さを \(L\) とすると、
\(L=\sqrt{a^2+b^2+c^2}\)
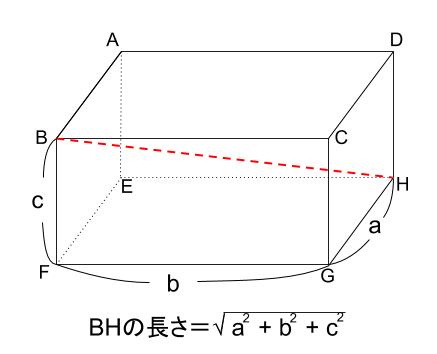
三平方の定理の斜辺の長さと似ていますね。
「三平方の定理の立体版」って感じがしますね。
なぜこの公式なのか
直方体の対角線の長さの公式は、なぜ成り立つのか。
これについては、公式の成り立ちまで学習しておくべきです。
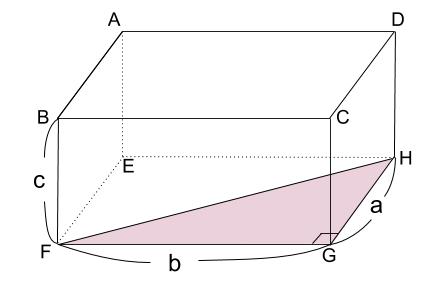
下の図の紫の三角形、
つまり直方体の底面の直角三角形 \(HFG\) について
三平方の定理を用いると
\(FH^2=a^2+b^2\)・・・①
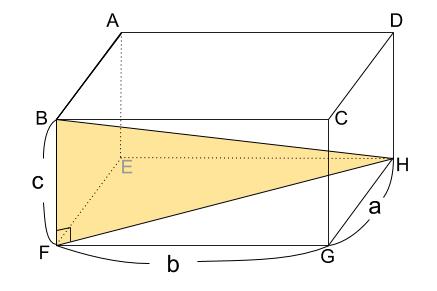
また、下の図のクリーム色の三角形、
つまり直方体の内部の直角三角形 \(BFH\) について
三平方の定理を用いると
\(BH^2=FH^2+c^2\)・・・②
①を②に代入すると
\(BH^2=a^2+b^2+c^2\)
\(BH \gt 0\) だから
\(BH=\sqrt{a^2+b^2+c^2}\)
これで、導けました。
空間図形も、平面に着目して解く
立体を扱うさいに、平面に着目するということが重要です。
上で見た、直方体の対角線の長さの公式の導出のように
\(1\) つずつ、平面で考えていくことが鍵になります。
例題
(1)縦 \(3cm\)、横 \(4cm\)、高さ \(5cm\) の直方体の対角線の長さを求めなさい。
(2)\(1\) 辺の長さが \(4cm\) の立方体の対角線の長さを求めなさい。
解答
この問題は、公式を適用して計算するだけです。
(1) \(\sqrt{3^2+4^2+5^2}\)
\(=\sqrt{9+16+25}\)
\(=\sqrt{50}\)
\(=5\sqrt{2}\)
(2) \(\sqrt{4^2+4^2+4^2}\)
\(=\sqrt{16+16+16}\)
\(=\sqrt{48}\)
\(=4\sqrt{3}\)
立方体の対角線
\(1\) 辺の長さが \(acm\) の立方体の対角線の長さは、
\(\sqrt{a^2+a^2+a^2}\)
\(=\sqrt{3a^2}\)
\(=a\sqrt{3}\)
公式として覚えてしまってもかまいません。
