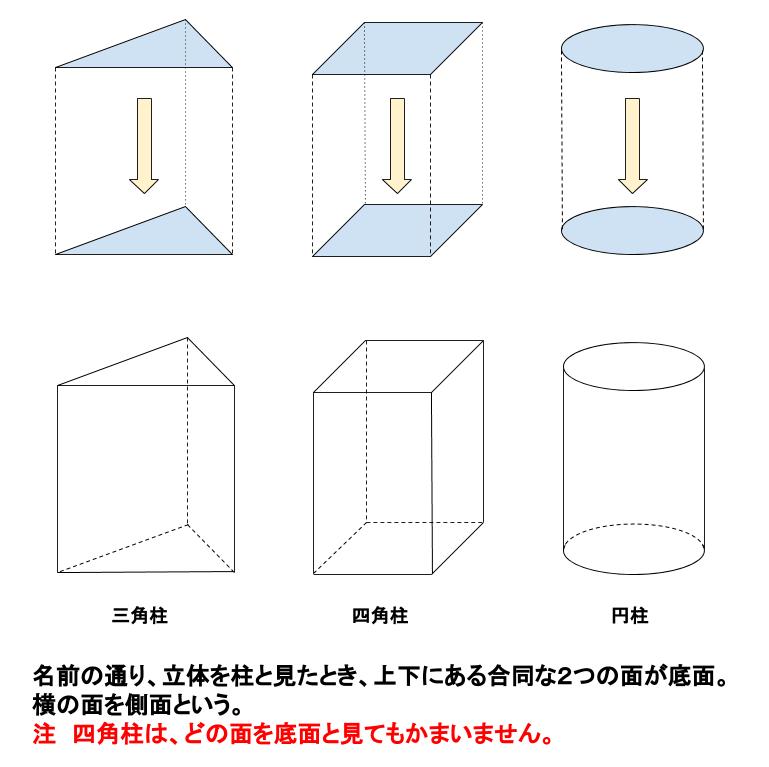
柱体
底面となる図形を、垂直に平行移動したとき、その通過した部分の立体を「柱体」といいます。
底面が三角形ならば、三角柱
底面が四角形ならば、四角柱(直方体ともいう)
底面が円ならば、円柱
となります。底面の形はどんな形でもかまいません。
底面という文字からは、底の面という印象を受けますが、上の面も底面です。
つまり、柱体の底面は2つあります。
また、底面でない部分を側面といいます。
体積の公式
\(柱体の体積=底面積×高さ\)
となります。
あらゆる柱体の体積を、この式で求めることができます。
底面の形がどんな形であってもです。
下の柱体 \(3\) つの体積を求めてみましょう。
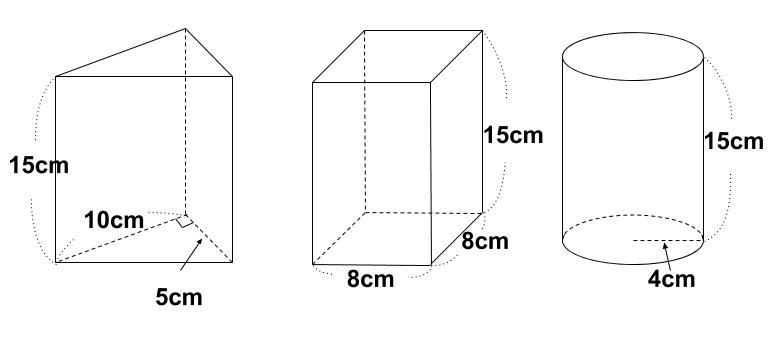
左の三角柱の体積
\(5×10×\displaystyle \frac{1}{2}=25(cm^2)\)・・・底面積
高さが \(15cm\) なので
\(25×15=375(cm^3)\)
もちろん、
\(5×10×\displaystyle \frac{1}{2}×15=375(cm^3)\)
でかまいません。
真ん中の四角柱(直方体)の体積
\(8×8×15=960(cm^3)\)
右の円柱の体積
\(4×4× \pi ×15=240\pi(cm^3)\)
柱体の表面積
\(柱体の表面積=底面積×2+側面積\)
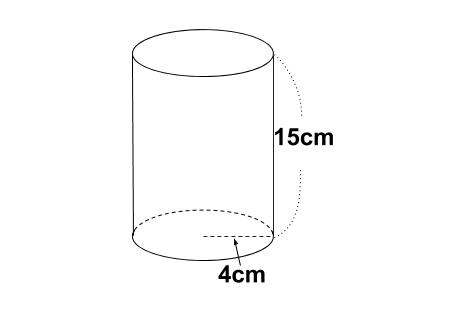
下の円柱の表面積を求めてみましょう。
表面積を求めるときは、立体の展開図を考えるとよいでしょう。
柱体の展開図は、缶詰を開けるように上下の底面をあけたのち、側面を切り開くのがおすすめです。
この切り開き方をすると、柱体は必ず、側面が長方形、その上下に底面が2つという展開図になります。
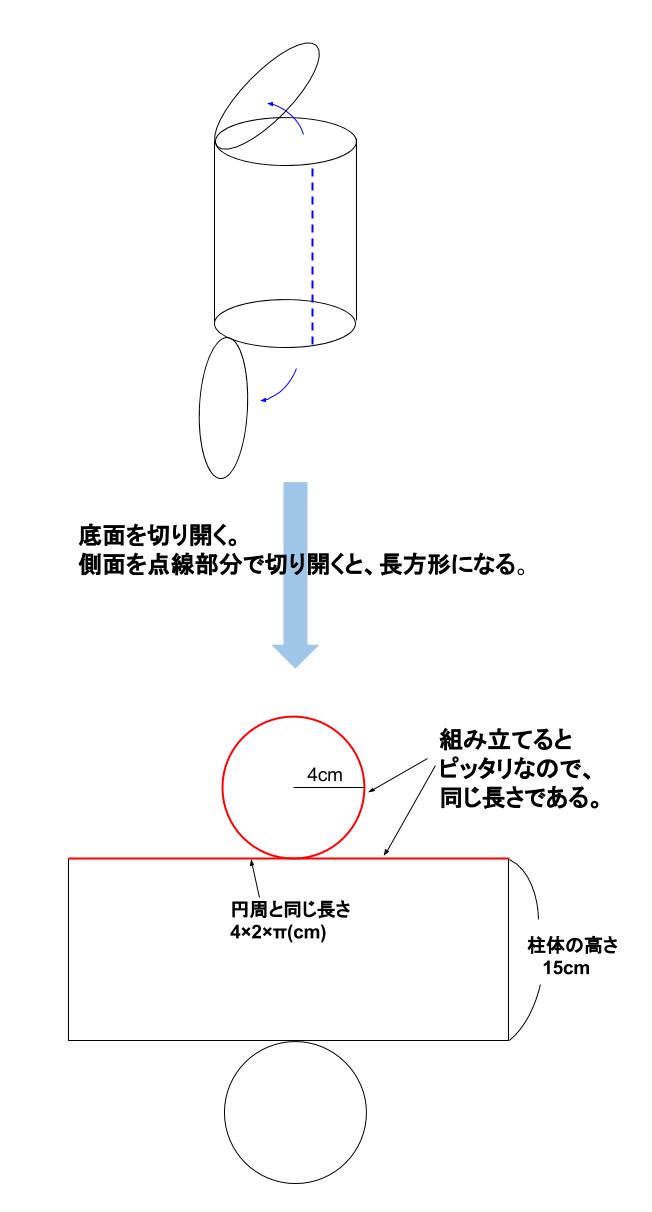
側面を切り開いてできる長方形の面積、すなわち側面積は、
側面積=立体の高さ × 底面の周の長さ
になります。
よって
側面積=\(4×2× \pi×15=120\pi(cm^2)\)
底面積は
\(4×4×\pi=16\pi(cm^2)\)
なので、
この円柱の表面積は
\(16\pi×2+120\pi=152\pi(cm^2)\)
と求まりました。
例題1
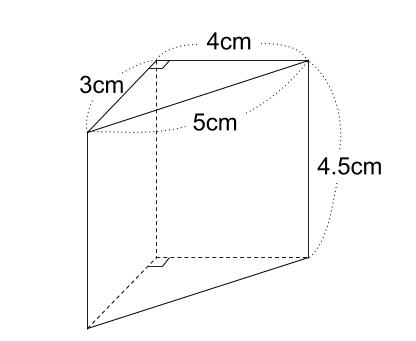
下の立体について
① 体積を求めなさい。
② 表面積を求めなさい。
解説
体積
直角三角形が底面で、
高さが \(4.5cm\) です。
よって、
体積=底面積×高さ
なので、
\(3×4× \displaystyle \frac{1}{2}×4.5=27\)\((cm^3)\)
表面積
展開図は下のようになります。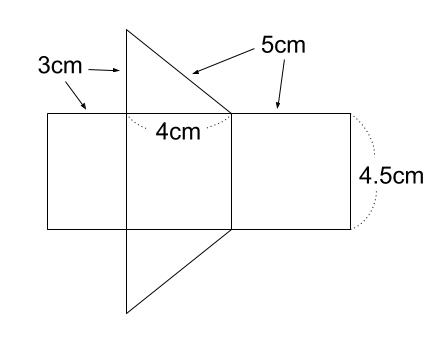
側面積は
たて \(4.5cm\)
よこ \(3+4+5=12(cm)\)
の長方形の面積として求められるので、
\(12×4.5=54(cm^2)\)
底面積は
\(4×3×\displaystyle \frac{1}{2}(cm^2)\)
なので、
求める表面積は
\(4×3×\displaystyle \frac{1}{2}×2+54=66(cm^2)\)
と求まります。
スポンサーリンク
