【中学数学】空間　平面と直線の位置関係

平面と平面の位置関係

空間内の2つの平面の位置関係は

• 平行　
• 交わる（特に垂直に交わるかどうかに注目）

この \(2\) 択となります。
交わる場合は、垂直であるか否かに注目することも多いです。

下の図を例に、平面と平面の位置関係を確認しましょう。

面と面が平行

面 \(ABCD\) と平行な面は面 \(EFGH\) です。
この \(2\) つの面をどの方向に無限に延長しても、交わることがありません。

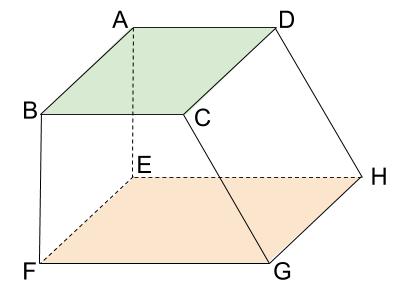
平面を無限に延長するとは下図のようなイメージです。

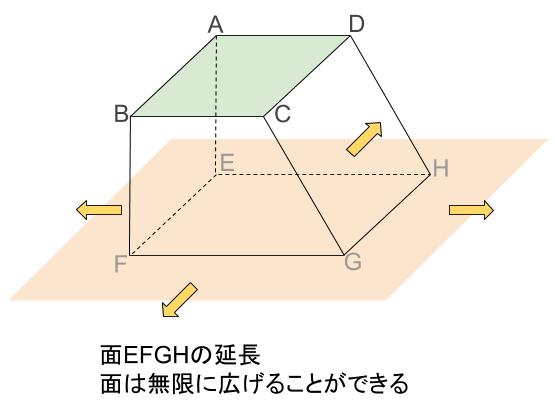
面と面が交わる

垂直に交わる

面 \(ABCD\) と垂直な面は面 \(ABFE\) です。

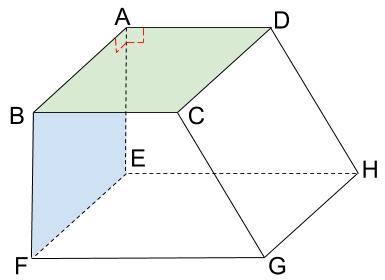
垂直でない交わり

面 \(ABCD\) と面 \(DCGH\) は交わっていますが、垂直ではありません。

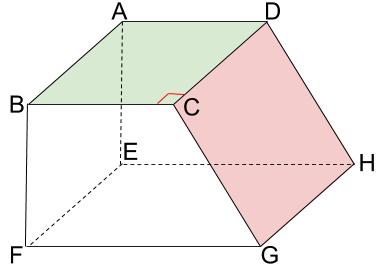
平面と直線の位置関係

空間内の平面と直線の位置関係は

• 平行　
• 交わる（特に垂直に交わるかどうかに注目）

この \(2\) 択になります。

下図の例で見ていきましょう。
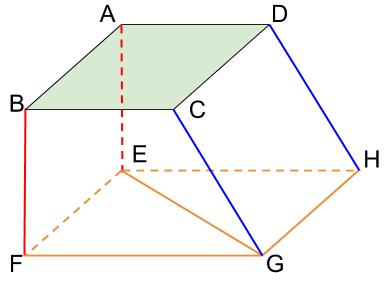
面 \(ABCD\) と平行な直線は黄色い線。
面や直線をどれだけ延長しても、決して交わることがないことがわかります。
平行な直線は、必ず平行な面内にある直線です。

面 \(ABCD\) と交わる直線は赤い線と青い線の両方であり、
垂直に交わっている直線は赤い線です。

直線と直線の位置関係

空間内の２直線の位置関係は

• 平行
• 交わる（特に垂直に交わるかどうかに注目）
• ねじれの位置

この３択になります。

ねじれの位置という新しい概念がでてきました。
どのようなものなのか、順に説明します。

交わるかどうかで判定

２直線が交わる

最もわかりやすいの交わる２直線です。

直線 \(AD\) と交わる直線は、下図の赤い線と青い線です。
その中で、垂直に交わる直線が赤い線です。

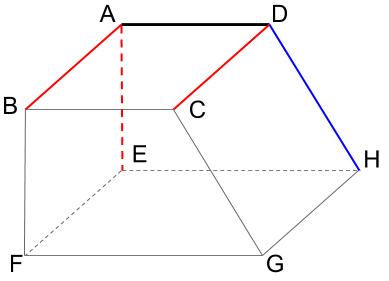
\(2\) 直線が垂直であるとは、その２直線を含む平面上で考えます
（この平面はただ \(1\) つに定まります）。
あとは、平面での垂直と同じことです。
例えば、面 \(AEHD\) に注目すると、\(AD\)と \(AE\) は垂直なので、
\(2\) 直線 \(AD\) と \(AE\) は垂直です。

２直線が交わらない

交わらない直線は
平行
ねじれの位置
のどちらかになります。

同一平面上にあるものが「平行」
それ以外が「ねじれの位置」です。

直線 \(AD\) に対して、
つまり赤茶色の直線が平行
紫の直線がねじれの位置です。

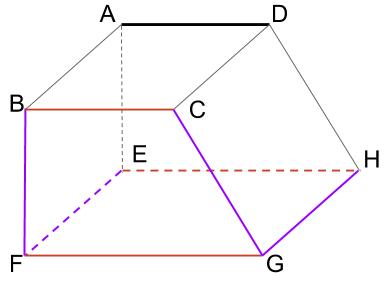
同一平面上かどうかで判定

ねじれの位置について、上のような見分け方を紹介しました。

しかし、「ねじれの位置」というのは、「同一平面上にない直線」のことなので、
２直線の位置関係の分類として、より適切なものは

１．２直線が同一平面上にあるか、ないか。
ないならば「ねじれの位置」
２．同一平面上にある２直線において、交わるか交わらないか。
交わらないならば「平行」

となります。
あまりこだわる必要はありませんが。

スポンサーリンク

• 次のページ 柱体