資料の整理
「資料の整理」においては、普段使わない言葉がたくさんでてきます。
度数、度数分布表、階級値、ヒストグラム、代表値・・・
実は、簡単なことをちょっと難しそうに言っているだけです。
とても簡単で、得点源となる「資料の整理」
高校入試においても、言葉の意味さえ知っていれば得点できるような
基本問題ばかりが出題されています。
しっかり学習して、得点源にしましょう!
度数の分布
度数分布表、階級
ある中学校では、\(1\) 年生全員の \(150\) 人に、数学の実力テストをしました。
その結果が以下の表です。
得点順に並べたものです。
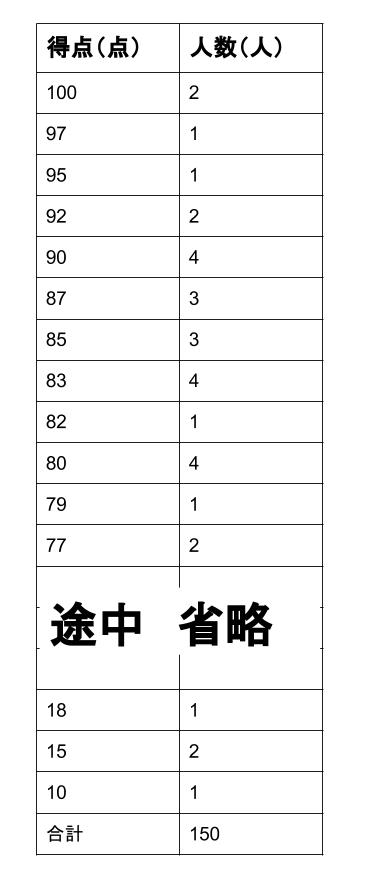
今回の例では、生徒 \(1\) 人 \(1\) 人の点数が「資料」です。
この「資料」をいかに整理して、扱いやすくするか。
「資料」から得られる情報は何か、
これが「資料の整理」という単元で学ぶ内容です。
「データの整理」と思ってください。
資料=データ
です。
さて、\(150\) 個の点数がズラッと並んだものを見ても、
うまくその情報を扱えません。
情報量が多すぎるのです。
上手にこの数値を整理して、意味のある情報を得ましょう。
まず、大雑把に生徒を得点ごとにグループわけします。
例えば以下のようになります。
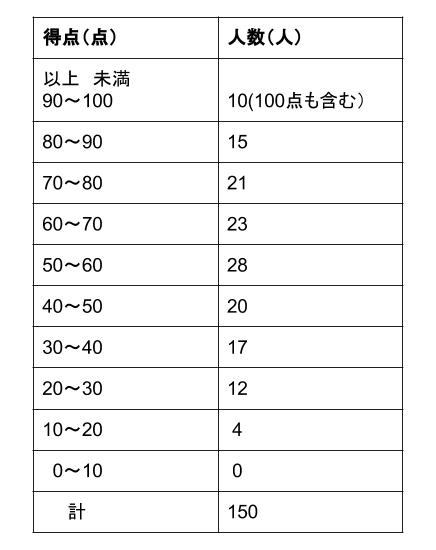
このような情報整理の表を
度数分布表といいます。
度数分布表の \(1\) つの区間を階級といい、
各階級の資料の個数を度数といいます。
上の例においては、
\(90~100\) の階級の度数は \(10\)
\(80~90\) の階級の度数は \(15\)
\(70~80\) の階級の度数は \(21\)
となっています。
階級の幅をいくつにするのかで、度数分布表への情報のまとめ方が変わります。
階級の幅が \(20\) の度数分布表を作成してみると
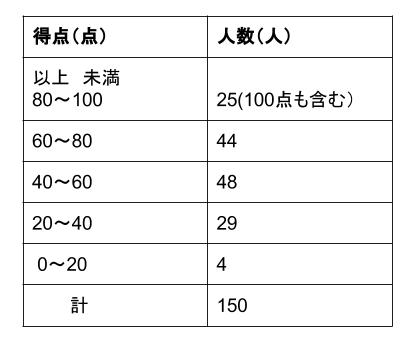
となります。
階級の幅が広くなると、表はとても簡潔にまとまります。
パッと見て、得点の分布をすぐに大雑把にとらえることができます。
その代わりに、情報の正確性は失われます。
階級の幅が狭ければ、より正確な情報に近づきますが、
大雑把に全体をとらえることが難しくなります。
一長一短があるのです。
資料の整理には、適度な幅が求められます。
階級値
いずれにしろ、 度数分布表にまとめた時点で、各資料の「真の値」は消えてしまいます。
結局、\(90~100\) の間にいる \(11\) 人の点数がいくつずつだったのか、その情報は消えてしまいます。
そこで、度数分布表だけが与えられた状況においては、
この \(11\) 人の点数は階級のまん中の値である、\(95\) 点であるとみなします。
これを階級値といいます。
ヒストグラム
小学校でも学習した棒グラフですが、
中学数学においてはこれをヒストグラムといいます。
棒グラフでいいじゃないですか・・・
先ほどの中学 \(1\) 年生の数学のテストを例に、ヒストグラムを学習しましょう。
階級の幅が \(10\) の度数分布表をもとに、ヒストグラム(棒グラフ)にします。
※度数分布表を再掲します。

今回のヒストグラムはこのようになります。
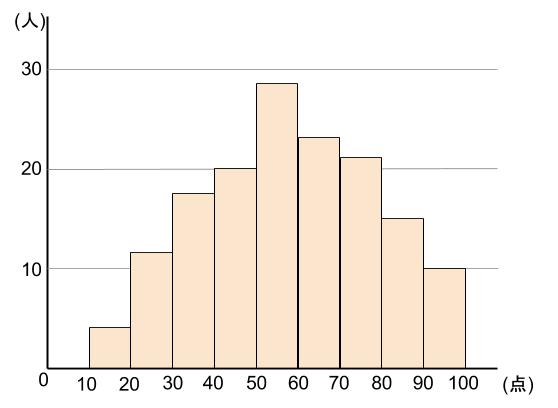
度数分布表とヒストグラムを見比べやすい、小さいバージョンも載せておきます↓
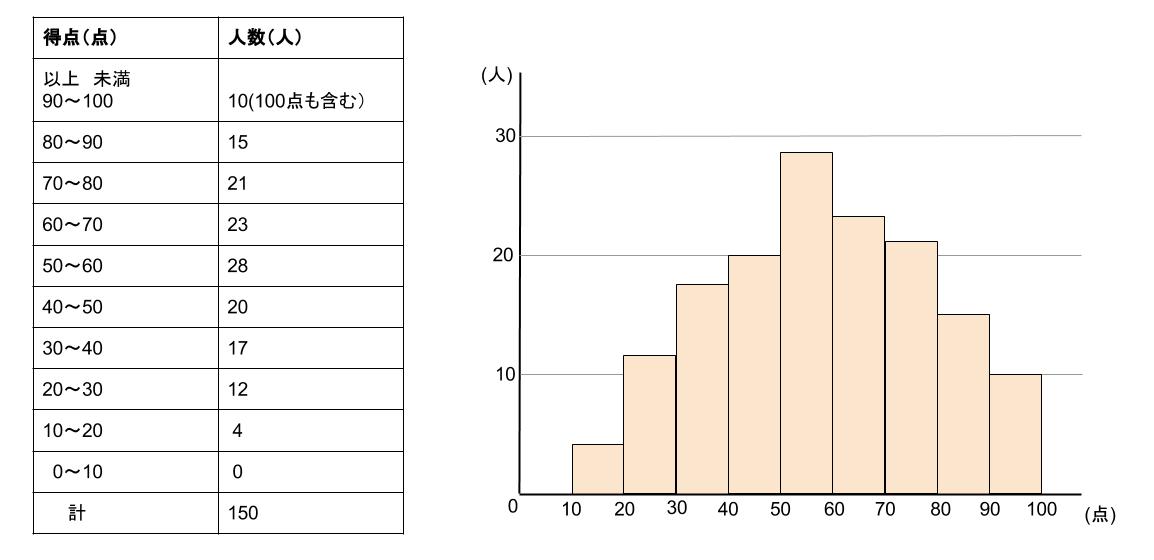
ヒストグラムのかき方や読みとり方は小学校の棒グラフと同じです。
念のために確認しておくと、
例えば、度数分布表における
\(40~50\) の階級の度数は \(20\) です。
※\(40\) 点以上 \(50\) 点未満の生徒が \(20\) 人いたということですね。
その他、\(10\) 個の階級をグラフ化することで、
ヒストグラムの完成となります。
ヒストグラムのように、グラフ化することで、
パッと見て資料の特徴がわかります。
視覚化することで特徴をとらえやすくなるのです。
例えば、英語のテストの結果を同様にヒストグラムにしたら
下のようだったとします。
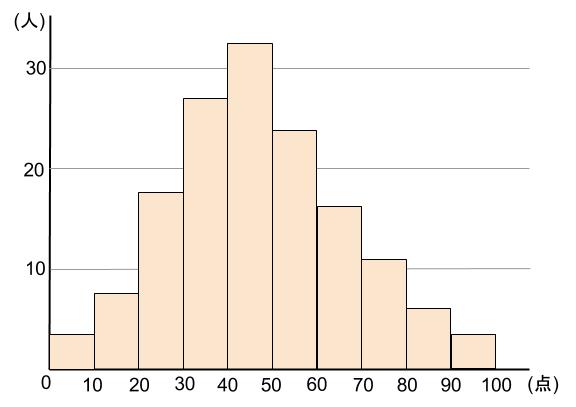
数学との違いが一目瞭然ですね。
英語は明らかに平均点が低いでしょう。
難しく作りすぎてしまったテストといえます。
相対度数
相対度数という言葉もあります。
これも、すごく簡単なのになんだか専門用語で
難しく感じるだけのものです。
相対度数の定義は、
\(相対度数=その階級の度数 / 度数の合計\)
なのですが、これって結局、「全体に対する割合」のことです。
例題
またまた、数学のテストの度数分布表に登場してもらいます。

\(80~90 \) の階級の相対度数を求めなさい。
解説
全 \(150\) 人のうち、\(80~90 \) の階級に当たる人数は \(15\) 人です。
この \(15\) 人が全体に対してどれくらいいるのか割合で表せば、
それが相対度数です。
\(15÷150=0.1\)
より、\(0.1\) です。
相対度数は普通、小数を用いて表します。
※\(10\)%の人がこの階級にいるということですね。
相対度数とは、全体に対する割合のことです。
難しく考える必要はありません。
スポンサーリンク
