方程式を成り立たせる値を、方程式の「解(かい)」といい、解を求めることを、「方程式を解く」といいます。
等式の変形
ただの逆算では解けない方程式がある
さて、小学生の時にやった「逆算」が、実は方程式であったことを紹介しましたが、
方程式のすべてを小学生のときにやったわけではありません。
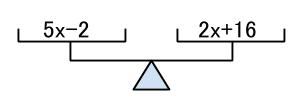
例えば以下の方程式
次の方程式を解け
\(5x-2=2x+16\)
これは小学校の時にはやっていません。
新しい手法を用いて、方程式を解きます。
それは超重要事項、等式の変形です。
「等式の変形=方程式の変形」と思ってもらってかまいません。
さて、等式の変形(方程式の変形)を学習してきましょう。
等式の変形 等式とはてんびんのつりあいである。
等式とは、左辺と右辺が等しいことを表しています。
理科のてんびんを想像してください。
てんびんがつりあっている状態、これが等式です。
例えば、このてんびんの両方の皿にまったく同じ重りを追加したら・・・
てんびんのつりあいは保たれたままです。
つりあっているてんびんの、左の皿と右の皿にまったく同じ操作をする。
もちろんつりあいは保たれ続けます。
また、左右を入れかえてもつりあいは保たれます。
等式のつりあいを保ったまま変形する方法5つ
- 両辺に同じ数を足す
- 両辺から同じ数を引く
- 両辺に同じ数をかける
- 両辺を同じ数で割る ただし、0で割ることはできない。
- 左辺と右辺を入れかえる
このように「つりあいを保ったまま式を変形」していって、「\(x=\)数値」の形になるまで変形すれば、方程式が解けたことになります。
具体例で見てみましょう。
さきほどの方程式を解いてみましょう。
\(5x-2=2x+16\)
両辺に2を足すと
\(5x-2\) \(+2\) \(=2x+16\) \(+2\)
左辺と右辺をそれぞれ計算して整理すると、
\(5x=2x+18\)
両辺から \(2x\) を引くと
\(5x\)\(-2x\)\(=2x+18\)\(-2x\)
左辺と右辺をそれぞれ計算して整理すると、
\(3x=18\)
両辺を3で割って・・・
\(x=6\)
このように解が求まりました。
つまり、てんびんがより簡略になるように、
左右に操作をしていきます。
\(x=数値\)
まで変形できれば、方程式が解けたことになります。
等式の変形で簡単な方程式を解いてみよう
さて、小学生時にやっていた逆算たちも立派な方程式であり、
等式の変形で解を求めることが可能です。
確認しておきましょう。
例題1
\(x+4=7\)・・・両辺から4をひく
\(x+4\)\(-4\)\(=7\)\(-4\)
\(x=3\)
例題2
\(2x-1=5\)・・・両辺に1を足す
\(2x-1\)\(+1\)\(=5\)\(+1\)
\(2x=6\)・・・両辺を2で割る
\(x=3\)
例題3
\(4x+12=20\)・・・両辺を4で割る
\((4x+12)×\)\(\frac{1}{4}\)\(=20×\)\(\frac{1}{4}\)
\(x+3=5\)・・・両辺から3をひく
\(x=2\)
別解
\(4x+12=20\)
\(4x+12-12=20-12\)
\(4x=8\)
\(x=2\)
例題4
\(0.1x+1.2=0.4\)・・・両辺を10倍する
\((0.1x+1.2)\)\(×10\)\(=0.4\)\(×10\)
\(x+12=4\)
\(x=-8\)
等式の変形で方程式を解く
さて、いよいよ中学生ならではの方程式を解きましょう。
それはつまり、等式の変形の練習をするということです。
例題
次の方程式を解きなさい。
(1)\(x=3x-8\)
(2)\(4x+3=-x+5\)
(3)\(-2-3x=\displaystyle \frac{x}{2}+1\)
解説
両辺に同じ計算をして、等式を変形していきます。
(1)\(x=3x-8\)
両辺に、どのような計算をするのか、
答えまでの道のりは \(1\) つではありません。
正しく式変形ができれば、どのような道を辿ってもOKです。
解答例1
\(x=3x-8\)
両辺から\(x\) を引くと、
\(x\)\(-x\)\(=3x-8\)\(-x\)
左辺、右辺を整理すると、
\(0=2x-8\)
両辺に \(8\) を足すと
\(0\)\(+8\)\(=2x-8\)\(+8\)
左辺、右辺を整理すると、
\(8=2x\)
両辺を \(2\) で割ると
\(8\)\(÷2\)\(=2x\)\(÷2\)
左辺、右辺を整理すると、
\(4=x\)
左辺と右辺を入れかえて
\(x=4\)
これで解が求まりました。
他にも、解にいたる道はいくらでもあります。
(2)\(4x+3=-x+5\)
変形途中を、(1)よりは少し省略していきます。
解答例
\(4x+3=-x+5\)
両辺に \(x\) を足すと
\(4x+3\)\(+x\)\(=-x+5\)\(+x\)
左辺、右辺を整理すると、
\(5x+3=5\)
両辺から \(3\) を引くと
\(5x+3\)\(-3\)\(=5\)\(-3\)
\(5x=2\)
両辺を \(5\) で割ると
\(x=\displaystyle \frac{2}{5}\)
これで解が求まりました。
(3)\(-2-3x=\displaystyle \frac{x}{2}+1\)
変形途中を、(1)よりは少し省略していきます。
解答例1
\(-2-3x=\displaystyle \frac{x}{2}+1\)
両辺から \(\displaystyle \frac{x}{2}\) を引くと
\(-2-\displaystyle \frac{7x}{2}=1\)
両辺に \(2\) を足すと
\(-\displaystyle \frac{7x}{2}=3\)
両辺を \(-2\) 倍すると
\(7x=-6\)
両辺を \(7\) で割ると
\(x=-\displaystyle \frac{6}{7}\)
これで解が求まりました。
解答例2
\(-2-3x=\displaystyle \frac{x}{2}+1\)
両辺を \(2\) 倍すると
\(-4-6x=x+2\)
両辺から \(x\) を引くと
\(-4-7x=2\)
両辺に \(4\) を足すと
\(-7x=6\)
両辺を \(-7\) で割ると
\(x=-\displaystyle \frac{6}{7}\)
これで解が求まりました。
スポンサーリンク
