円周の長さと円の面積
小学校で学習した、円周の長さ、円の面積、これらを求める公式の復習からです。
円周の長さ = 直径 × 円周率(およそ3.14)
円の面積 = 半径 × 半径 × 円周率
この \(2\) つの公式は、なにはともあれ絶対に「丸暗記」です。
円周率
円周率とは、無限に続く小数であり、およそ \(3.141592・・・\)
という値です。
小学校のときは、円周率を \(3.14\) として計算しなさい、
ということが多かったと思います。
数学では、円周率を \(\pi\) という文字で表します。
パイと読みます。
これを用いて数学では、円周の長さ(\(L\) とします)の公式、円の面積(\(S\) とします)の公式は以下のようになります。
円周の長さ \(L=2\)\(\pi\)\(r\) (に パイ アール と読みます。)
円の面積 \(S=\)\(\pi\)\(r^2\) (パイ アール 2乗 とよみます。)
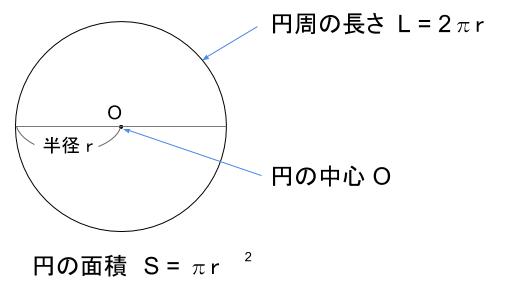
別にこの中学校式表示は覚えなくとも問題はありません。
実際に計算するときは、小学校のときのように \(2\) 乗を用いない方が
約分がやりやすいことも多いです。
おうぎ形
円を、\(2\) つの半径で切り取ったものを「おうぎ形」といいます。
おうぎ形も小学校ですでに習っているものですね。
\(2\) つの半径のなす角を、中心角
円周の一部を弧
といいます。
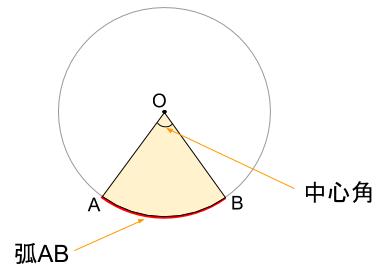
おうぎ形は円の一部であり、以下の公式も「円の一部」という意味の式になっています。
\(弧の長さ=円周×\)\(\frac{中心角}{360}\)
\(おうぎ形の面積=円の面積×\)\(\frac{中心角}{360}\)
おうぎ形の公式にある、\(\frac{中心角}{360}\) 倍は、割合・比の考え方です。
苦手としている人もいるでしょうから、くわしくおさらいしておきましょう。
例題
半径が \(8cm\) 、中心角が \(75°\) のおうぎ形の面積を求めなさい。
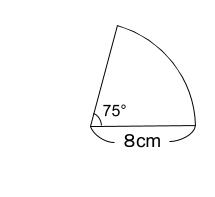
解答
公式にあてはめて計算するのみです。
\(8×8×\pi ×\displaystyle \frac{75}{360}\)\(=\displaystyle \frac{40}{3}\)\(\pi\)
より、\(\displaystyle \frac{40}{3}\)\(\pi(cm^2)\)
これは、円の面積の \(\displaystyle \frac{75}{360}\) 倍であるという意味の公式です。
比の言葉で表すと、円とおうぎ形の面積の比が \(360:75\) ということです。
なぜ \(360\) がでてくるのか。
これは、\(1\) 回転の角度が \(360°\) だからです。
円が、中心角が \(360°\) のおうぎ形ということです。
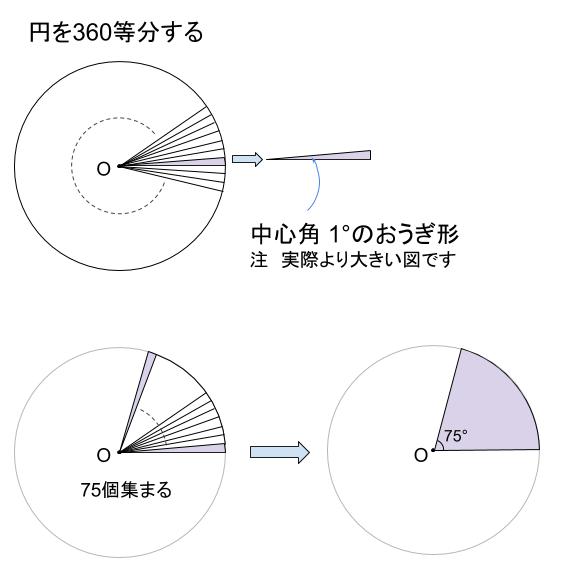
円を \(360\) 等分すると、中心角が \(1°\) のおうぎ形になります。
この面積は 円の面積 × \(\displaystyle \frac{1}{360}\)
この中心角 \(1°\)のおうぎ形が \(75\) 個集まると、その面積は
円の面積\(×\displaystyle \frac{1}{360}×75\)
これがおうぎ形の公式の意味するところです。
おうぎ形の面積 もう1つの方法
おうぎ形の面積には、もう \(1\) つ覚えておいて損のない公式があります。
おうぎ形の半径を \(r\) 、弧の長さを \(l\) とすると、面積 \(S\) は、
\(S=\)\(\displaystyle \frac{1}{2}\)\(lr\)
となります。
直感的な理解
直感的な覚え方としては「三角形」と「おうぎ形」って似てるでしょ!
というもので、どちらの面積も、
\(面積=底辺×高さ×\)\(\displaystyle \frac{1}{2}\)
で求まるというものです。
下図のように捉えます。

厳密に数学的な理解
ちゃんと説明すると以下のようになります。
\(\displaystyle \frac{1}{2}\)\(lr\)・・・①
が
\({\pi} r^2 ×\)\(\displaystyle \frac{x}{360}\)・・・②
と等しいことを示したいわけです。
ところで、弧の長さの公式より、
\(l=2{\pi} r ×\)\(\displaystyle \frac{x}{360}\)
なので、これを①式に代入すると
\(\displaystyle \frac{1}{2}\)\(lr\)
\(=\displaystyle \frac{1}{2}\)\(×2{\pi}r×\)\(\displaystyle \frac{x}{360}\)\(×r\)
\(={\pi}r^2×\)\(\displaystyle \frac{x}{360}\)
これで示すことができました。
この公式は、中心角が何度であっても使用可能ですし、円にも使用可能です。
スポンサーリンク
