ひし形の性質
ひし形の作図は、中学数学における作図の最重要事項です。
なぜなら、中学数学の作図の \(2\) 大重要暗記事項は
- 垂直二等分線の作図
- 角の二等分線の作図
なのですが、いずれもひし形の作図から達成できるのです。
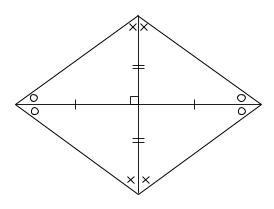
ひし形の図形的性質として、
- ひし形の対角線は、垂直にかつ、中点で交わる。
- ひし形の対角線は、内角を二等分する。
があるからです。
以下、垂直二等分線の作図方法と角の二等分線の作図方法を学習します。
すべて理解した上で、暗記をしなくてはなりません。
垂直二等分線の作図
例題1
線分 \(AB\) の垂直二等分線を作図しなさい。

解答
どのような線を作図するのか、まず目標を定めることが大事です。
ラフスケッチしましょう。

これって・・・・ひし形の一部じゃないですか!!
ひし形の対角線が最終的な解答です!
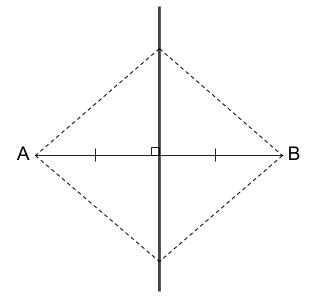
よって、ひし形の作図をします。
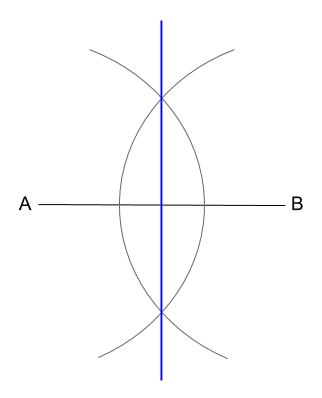
\(A,B\) を中心とする半径の等しい円をかけば、ひし形の作図です。
暗記していますね?
もちろん \(4\) つの辺はかきません。
青い太線が、求める垂直二等分線です。
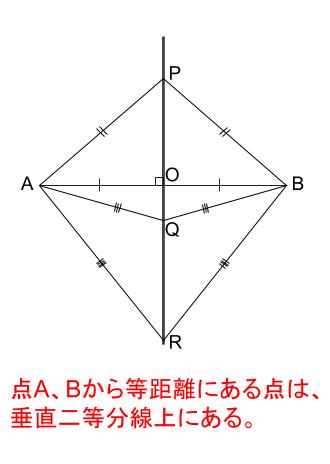
\(2\) 点からの距離が等しい直線は垂直二等分線
垂直二等分線は、点 \(A,B\) から等距離にある点の集合です。
単純に、「 \(2\) 点からの距離が等しい直線は垂直二等分線」ともいいます。
角の二等分の作図
例題2
\(\angle A\) の二等分線を作図しなさい。
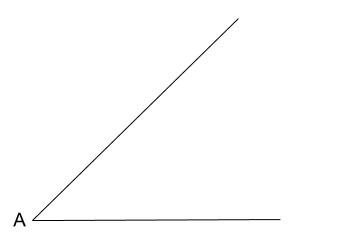
解答
どのような線を作図するのか、まず目標を定めることが大事です。
ラフスケッチしましょう。

これって・・・・ひし形の一部じゃないですか!!
よって、ひし形の作図をします。
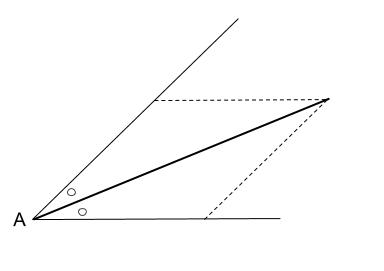
よって、ひし形の作図をします。
もちろん \(4\) つの辺はかきません。
青い太線が、求める角の二等分線です。
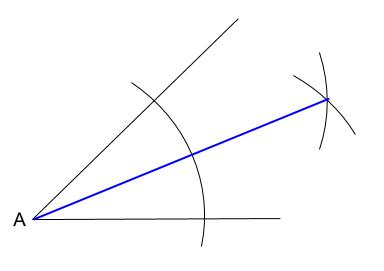
\(2\) 辺からの距離が等しい直線は角の二等分線
角の二等分線は、\(2\) つの直線から等距離にある点の集合です。
単純に、「\(2\) 辺からの距離が等しい直線は角の二等分線」ともいいます。
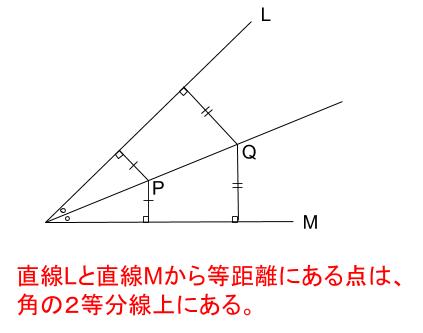
垂直二等分線の作図と角の二等分線の作図。
必ず暗記しましょう。
これがすべての作図に通ずる超重要事項です!
必ず暗記しましょう。
これがすべての作図に通ずる超重要事項です!
スポンサーリンク
