代表値・平均値
引き続き「資料の整理」です。
使い慣れない言葉の意味さえ覚えれば、あとは難しいことはありません。
確実に得点源にしましょう。
範囲
資料の最大から最小を引いた値を 範囲といいます。
例
生徒 \(8\) 人のある期間の読書数(冊)
\(4 , 5 , 2 , 0 , 2 , 5 , 9 ,1 \)
最大は \(9\) 冊、
最少は \(0\) 冊
\(範囲=9-0=9\)
となります。
代表値
資料の特徴を表す値を
代表値といいます。
平均値、最頻値、中央値
などがあります。
このページでは、「平均値」について学習しましょう。
平均値
平均とは平らに均す(ならす)こと
まずは、よく知っている平均です。
\(平均値=資料の値の合計÷資料の個数\)
となります。
例
生徒 \(8\) 人のある数学のテストの得点(点)
\(42 , 55 , 72 , 80 , 62 , 75 , 90 ,65 \)
\(8\) 人の、この数学のテストの平均点を求めます。
\(8\) 人の平均点は、
\(8\) 人のテストの点数の合計を \(8\) で割れば求まります。
\(8つの資料の合計\)\(=42+55+72+80+62+75+90+65=541\)
資料の個数は \(8\)
よって、
\(平均値=541÷8=67.625\) (点)
となります。
平均とは平らに均す(ならす)という意味で、
\(8\) 人全員が同じ点数だったら?
という考え方の値です。
同じテストを受けた別の人たち、\(20\) 人がいて
その人たちの点数の合計が \(1290\) 点でした。
どちらが優秀な集団でしょうか?
合計点では決められませんね。人数が多い方が有利です。
\(20\) 人の平均を取れば、
\(1290÷20=64.5\)(点)
少しだけ、 \(8\) 人の集団の方が優秀です。
このように、平均値をとることで、全資料の大まかな性質を
見ることができます。
仮の平均
「仮の平均」という考え方を用いると、平均値を出すための計算が楽になることがあります。
ますは、簡単な例で「仮の平均」の意味を学習しましょう。
例
\(43,48,41\) の平均を求めなさい。
もちろん平均値は
\((43+48+41)÷3=44\)
です。
これを仮の平均を用いて計算すると以下のようになります。
「仮の平均」を \(43\) として、そこからの増減は、
\(43\) は \(+0\)
\(48\) は \(+5\)
\(41\) は \(-2\)
仮の平均 \(43\) からの増減分のみの平均をだします。
\((0+5-2)÷3=1\)
よって、「真の平均」は「仮の平均」の \(43\) から \(+1\) ずれています。
\(43+1=44\)
これで、平均値が求まりました。
平均とは平らに均すことです。
凸凹(でこぼこ)な道を平らにする土木工事に例えられます。
「仮の平均」は、凸凹(でこぼこ)の部分だけ工事すれば良い、という考え方です。
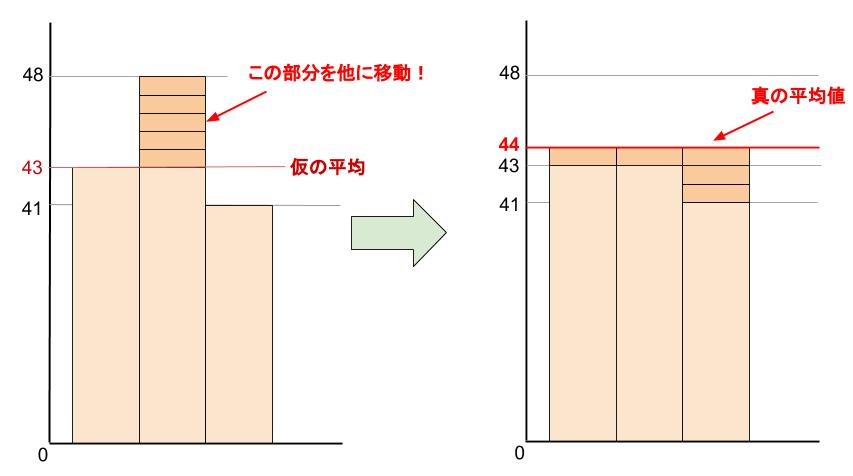
今回、「仮の平均」を \(43\) としましたが、
「仮の平均」はいくつであってもOKです。
計算が楽になりそうな値を適当にとります。
例2
この考え方を、先の \(8\) 人の数学のテストに適用してみましょう。
生徒 \(8\) 人のある数学のテストの得点(点)
\(42 , 55 , 72 , 80 , 62 , 75 , 90 ,65 \)
この \(8\) 人の平均点を求めます。
仮の平均を何点にすると計算が楽になりそうか・・・
直感で構いません。だいたい平均になりそうな値を選ぶと良いでしょう。
今回は仮の平均を \(65\) としてみます。
\(42\) は \(-23\)
\(55\) は \(-10\)
\(72\) は \(+7\)
\(80\) は \(+15\)
\(62\) は \(-3\)
\(75\) は \(+10\)
\(90\) は \(+25\)
\(65\) は \(+0\)
この \(8\) つのずれの合計を出します。
合わせて \(0\) に近くなる \(2\) つ、あるいは \(3\) つを組みにすると良いです。
つまり、
\(+25\) と \(-23\) で \(+2\)
\(+10\) と \(-10\) で \(+0\)
あとは \(+7\) 、\(+15\)、\(-3\)、\(+0\) が残ってます。
合わせて \(+19\)
以上より、
\(+2\) と \(+0\) と \(+19\) で合わせて \(21\)
よってずれの平均は
\(21÷8=2.625\)
つまり仮の平均 \(65\) から \(+2.625\) ずれているので
\(65+2.625=67.625\)
これで平均が求まりました。
どうでしょう?
はっきり言って、「仮の平均」の利用によって
ものすごく楽になったとは言えませんね。
「仮の平均」を使わないで計算した方が速いかもしれません。
使った方が楽になりそうか、使わないほうが楽そうか。
考えてから計算をはじめましょう。
度数分布表からの平均
度数分布表から、全資料の平均値をだすこともあります。
度数分布表からは、各資料の本当の値はわかりません。
よって、各階級の資料の値はすべて階級値として計算し、平均値を求めます。
※つまり、おおよその値を出すということになります。
例
\(A\) さんの走り幅跳び \(20\) 回の記録の平均を求めなさい。
\(A\) さんの走り幅跳びの記録
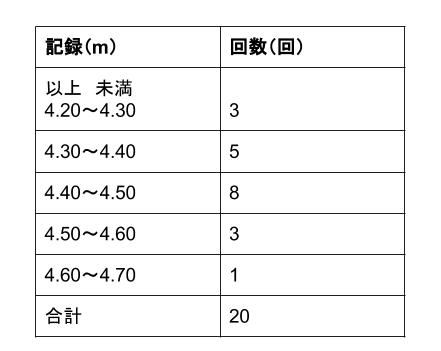
解説
度数分布表からは、各資料の本当の値はわかりません。
\(A\) さんが何 \(m\) 跳んだのか、本当の値は \(1\) つもわからないのです。
よって、階級値を用います。
度数分布表から以下のように情報を読みとります。

より、\(A\) さんが \(20\) 回で跳んだ距離の合計を求めます。
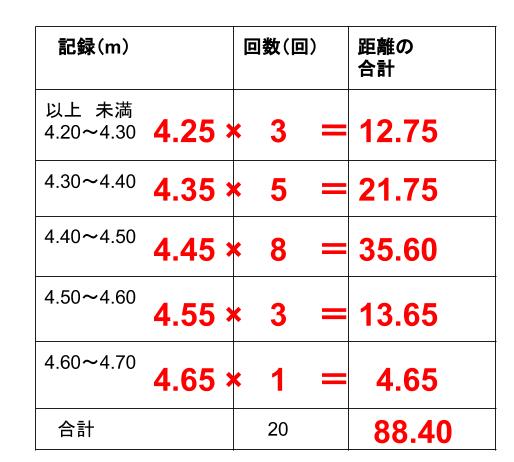
\(20\) 回の合計距離 \(88.40\) を回数 \(20\) で割れば、
平均が求まります。
\(88.40÷20 =4.42(m)\)
となります。
仮の平均の利用が圧倒的に楽
上の計算はなかなか面倒でしたね。
これは「仮の平均」を用いると楽になるところでしょう。
「仮の平均」を \(4.45\) としてみましょう。
もっとも回数の多い階級の階級値です。
平均値はこのあたりになりそうですからね。
この \(4.45\) からのずれの合計を求めます。
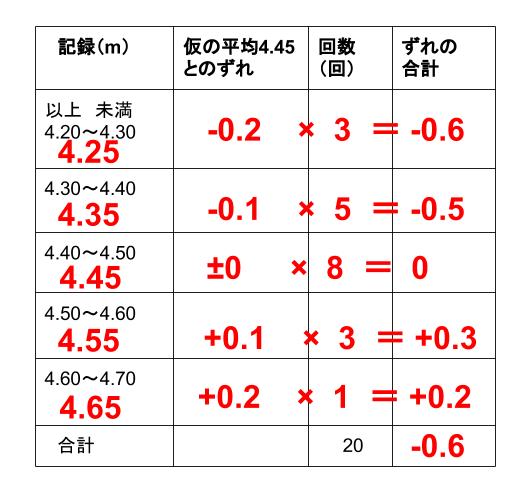
\(20\) 回のずれの合計は \(-0.6\) です。
\(1\) 回あたり
\(-0.6÷20=-0.03\)
より、「仮の平均」の \(4.45\) と \(-0.03\) ずれているので
\(4.45-0.03=4.42\)
今回は、絶対に仮の平均を利用すべき問題と言えます。
スポンサーリンク
