正負の数の加減のまとめ
今まで学習してきた、正負の数の加減を、総まとめにして頭の中を改めて整理しましょう。
正負の数の加減の計算ルール、手順
1、( )をはずして、正の数の加減にする。
正の数についた( )は無意味。ただはずすだけ。
負の数についた( )は注意深く、正確にはずす。
ルールは( )の前の演算記号を逆にする。
2、( )のない式になったら、あとは数直線で右方向、左方向を考える。
具体例で見ていきましょう。
正負の数の加減の具体例
例1
\((+4)\underline{-(+5)}\)・・・正の数の( )はそもそもいらない。( )や + をはずす。
\(=4\underline{-5}\)
\(=-1\)
例2
\(5\underline{+(-3)}\)・・・負の数は( )の前の演算記号を逆にして( )をはずす。
\(=5\underline{-3}\)
\(=2\)
例3
\(-4\underline{-(-1)}\)・・・負の数は( )の前の演算記号を逆にして( )をはずす。
\(=-4\underline{+1}\)
\(=-3\)
例4
\(\underline{(-1)}+6\)・・・式の先頭の負の数は、そのまま負の数とする。
\(=\underline{-1}+6\)
\(=5\)
3項、4項のときの加減の具体例
\(3\) つや \(4\) つやそれ以上の数を加減することを考えましょう。
例1
\(-3+5-4\)
このように( )がまったくない計算においては、
はじめから、
正の方向 →
と
負の方向 ←
のせめぎ合いを考えます。
→ は \(+5\)
← は \(-3\) と \(-4\)
つまり、右に \(5\) 進んだ後、左に \(3+4=7\) 進むのです。
到着する地点は \(-2\) です。
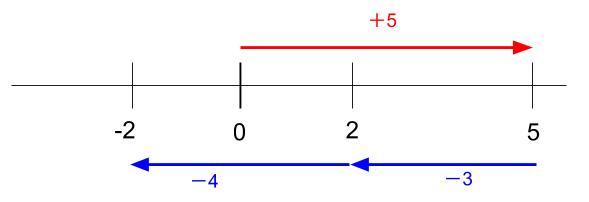
\(-3+5-4\)
\(=5-7\)
\(=-2\)
と答案に書いてOKです。
非の打ちどころのない解答です。
\(1\) 行目から \(2\) 行目への式変形ですが、これでぜんぜん問題ありません!!
例2
\(-4-(-3)+6-4+(-2)\)
まず( )のない式にします。
\(-4-(-3)+6-4+(-2)\)
\(=-4+3+6-4-2\)
このあとは→ と ← のせめぎあいです。
→に \(3+6=9\)
←に \(4+4+2=10\)
右に \(9\) 進んだ後、左に \(10\) 進めば、
到着地点は左に \(1\)
つまり、\(-1\) です。
\(-4-(-3)+6-4+(-2)\)
\(=-4+3+6-4-2\)
\(=9-10\)
\(=-1\)
と答案にかいてOKですよ!
例3
\(-2-(+3)+(-4)\)
\((+3)\) のような表現は、\(3\) が正の数であることを主張しています。
正の数なんですから、いままで小学生のときにやっていた通りの表現にするだけです。
( )なんてつけなかったし、プラスであることをあえて明記することもなかったですね。
つまり、
\(-2-(+3)\) は当然
\(-2-3\) のことなんです。
これだけのことです。
( )の外し方を呪文のようなルールで暗記するようなことはやめましょうね。
\(-2-(+3)+(-4)\)
\(=-2-3-4\)
すべて左方向に進め!ですね
\(=-9\)
まとめ
正負の数の加減の計算ルール、手順
1、( )をはずして、正の数の加減にする。
正の数についた( )は無意味。ただはずすだけ。
負の数についた( )は注意深く、正確にはずす。
ルールは( )の前の演算記号を逆にする。
2、( )のない式になったら、あとは数直線で右方向、左方向を考える。
→ と← のせめぎ合いを考えればOKです
