球の体積と表面積
半径 \(r\) の球の体積と表面積を求める公式は以下のようになります。
\(球の体積=\displaystyle \frac{4}{3}\pi r^3\)
\(球の表面積=4\pi r^2\)

「なぜこの公式が成立するのか」については中学生の知識の範囲外です。
証明には高校数学の「積分」という知識が必要です。
どうしても気になる人は、いろいろ調べてみてください。
ガヴァリエリの原理やハップス・ギュルダンの定理を用いた直感的説明が有名です。
※ガヴァリエリの原理やハップス・ギュルダンの定理の証明を無視すれば、の話です。
公式の覚え方
なにはともあれ、公式は暗記しましょう。
そして、それを使いこなせればとりあえずOKです。
※携帯電話の仕組みを知らなくても、使いこなせればいいのです。
内部の電気回路の仕組みを学習しませんね。
球の公式には、古くから伝わる有名なゴロ合わせがあります。
\(球の体積=\displaystyle \frac{4}{3}\pi r^3\)
身の上に心配あるので三乗
(\(3\) の上に \(4\pi r^3\))
\(球の表面積=4\pi r^2\)
心配ある事情
とても覚えやすいのですが、
どっちが体積でどっちが表面積が混乱する可能性があります。
見分け方ですが
体積は \(3\) 乗
面積は \(2\) 乗
です。
体積や面積の単位を思い出してください。
体積は \(cm^3\) のように、 \(3\) 乗なのです。長さ(\(cm\))を \(3\) 回かけ算すると体積になります。
面積は \(cm^2\) のように、 \(2\) 乗なのです。長さ(\(cm\))を \(2\) 回かけ算すると面積になります。
\(球の体積=\displaystyle \frac{4}{3}\pi r^3\)
ですが、\(1\) 辺の長さが \(r\) の立方体の体積 \(r^3\) の \(\displaystyle \frac{4}{3}\pi\) 倍
という意味です。 \(\displaystyle \frac{4}{3}\pi\) は単位のないただの比です。
\(球の表面積=4\pi r^2\)
ですが、\(1\) 辺の長さが \(r\) の正方形の面積 \(r^2\) の \(4\pi\) 倍という意味です。 \(4\pi\) は単位のないただの比です。
例題1
半径が \(6\) の球の体積と表面積を求めなさい。
解答
公式を適用するだけの問題です。
\(球の体積=\displaystyle \frac{4}{3}\pi r^3\) なので、
\(\displaystyle \frac{4}{3}\pi 6^3\)
\(=288\pi\)
\(球の表面積=4\pi r^2\) なので
\(4\pi 6^2\)
\(=144\pi\)
例題2
半径が \(3\) の半球の体積と表面積を求めなさい。
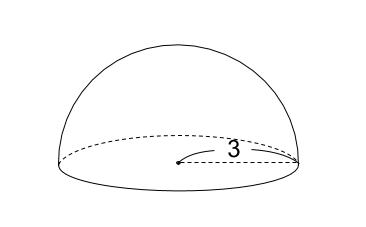
解答
半球とは図のように、球をちょうど半分にした立体です。
体積は、球の体積の半分なので
\(\displaystyle \frac{4}{3}\pi 3^3×\displaystyle \frac{1}{2}\)
\(=18\pi\)
表面積は、球の表面積の半分と切断面の面積の合計です。
球の表面積の半分は
\(4\pi3^2×\displaystyle \frac{1}{2}\)
\(=18\pi\)
切断面の面積は、半径 \(3\) の円の面積なので
\(\pi3^2\)
\(=9\pi\)
よって、求める表面積は
\(18\pi + 9\pi\)
\(=27\pi\)
例題3
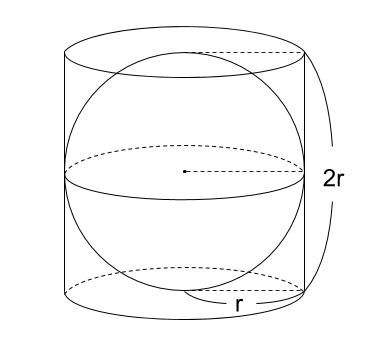
下の図のように、底面の半径が \(r\) で、高さが \(2r\) の円柱に
ぴったりと球が内接している(球の半径が \(r\) であるということ)
この球の表面積が \(100\pi \) のとき円柱の側面積を求めなさい。
解答
\(球の表面積 = 4\pi r^2\) なので
\(4\pi r^2=100\pi\)
これを解いて
\(r=5\) \((r \gt 0)\)
よって、円柱の半径が \(5\) 、髙さが \(10\) なので、
この円柱の側面積は
\(5×2×\pi×10\)
\(=100\pi\)
球の表面積と一致しました。
これは偶然ではなくて、半径がいくつであっても成り立ちます。
半径 \(r\)、高さ \(2r\) の円柱の側面積
\(r×2×\pi×2r\)
\(=4\pi r^2\)
これは、半径 \(r\) の球の表面積と一致する。
スポンサーリンク
