多面体
多面体
平面だけで囲まれた立体を多面体といいます。
※円柱や円すいは多面体ではありません。
正多面体
すべての面が合同な正多角形であり、どの頂点にも同じ数の面が集まっているへこみのない立体を「正多面体」という。
この文だけ読んでもピンとこないに決まっています。
下の正多面体の図を見ながら、「なるほどね」
と思ってもらえれば十分です。
直感的な言葉でかけば、
「正多面体とは、すべての面が合同な正多角形で、非常に対称的な立体」
です。
「非常に対称的な立体」という箇所が曖昧で、数学としてはダメな表現ですが、
理解の一助になると思います。
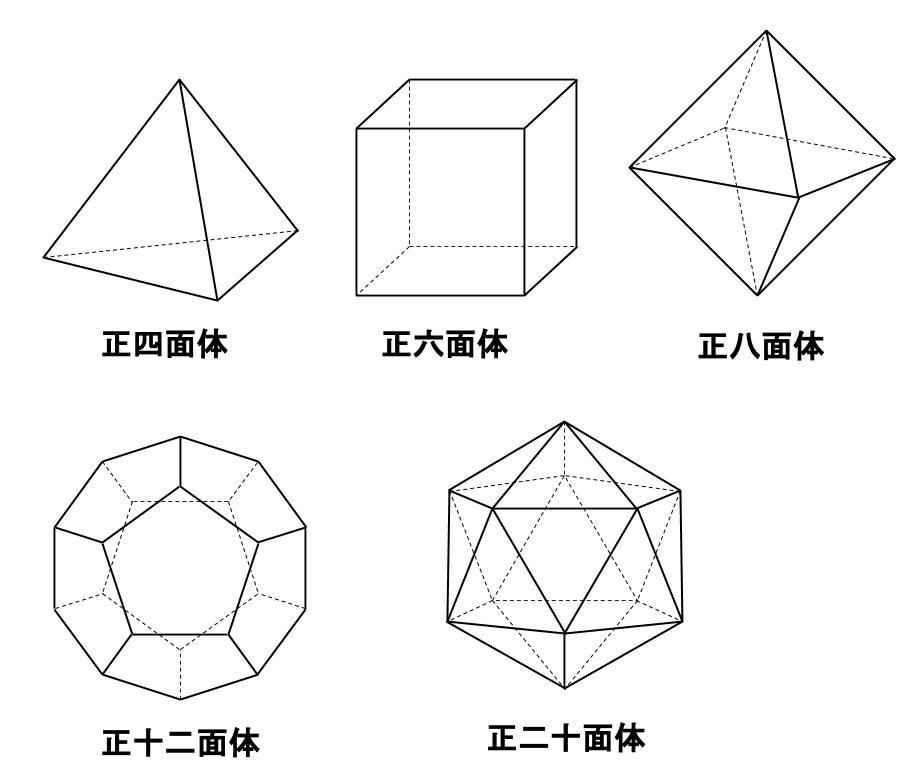
正多面体は、全部で5種類
正多面体は下図の \(5\) 種類です。
これですべてです。
正六面体とはもちろん立方体のことです。
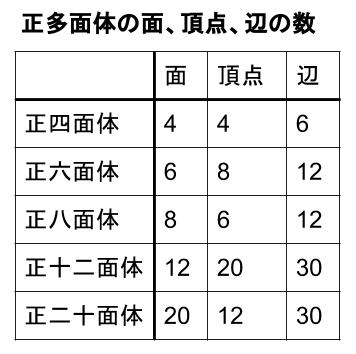
この表はテストにでますか、暗記ですか?
という疑問が頭の中にうかびますね。
ずばり、
1.この表は、テストや入試で問われることがある
2.だから、答えられるように準備しておくべきである
となります。
どんな準備をしておけばよいかというと、表をすべて丸暗記するのではなくて、
ほんの少しだけ暗記をしてもらおうと思います。
各正多面体がどのようなものか、概形は暗記!
上で図に示した通りですが、
各正多面体がおおよそどのような形なのかは知らないと話になりません。
特に、
正四面体、
正六面体
正八面体
の \(3\) つは、白紙に見取り図をかけるようになっておくべきです。
正十二面体、正二十面体の見取り図はかけなくともかまいませんが、
正十二面体の面は正五角形、
正二十面体の面は正三角形
であることは覚えてください。
オイラーの多面体定理
すべての多面体において、
\((面の数)+(頂点の数)-(辺の数)=2\)
が成り立ちます。
これをオイラーの多面体定理といいます。
もちろん正多面体にもこの定理は適用できます。
まずは、この定理を暗記してしまいましょう。
式変形をして、
\((面の数)+(頂点の数)=(辺の数)+2\)
と覚えても構いません。
覚えやすいように覚えてください。
※どうしても暗記が嫌だ!という人のために、この定理の暗記なしの方法も書きます。
最後まで読んでください。
※なぜこの定理が成り立つの???もっともな疑問ですが、この証明は本サイトのレベルを超えるものと判断し、割愛します。
正多面体の辺の数の導出
各正多面体の面の数は改めて暗記するようなことではありません。
正 \(N\) 面体の面の数は \(N\) ですから。
あたりまえですね。
ですので、オイラーの多面体定理さえ覚えておけば、あとは「辺の数」か
「頂点の数」のどちらかさえわかれば、残り片方もわかります。
おススメするのは「辺の数の導出方法の暗記」です。
「導出方法」なんか覚えなくたって、各多面体の辺の数は少ない順に、
\(6,12,12,30,30\) とかなり覚えやすいから、これくらい暗記で済ませるよ、という方法もあります。
これを一概に否定することはできませんが、「辺の数の導出方法の暗記」はぜひ学習して欲しいと思います。
例 正六面体(立方体)
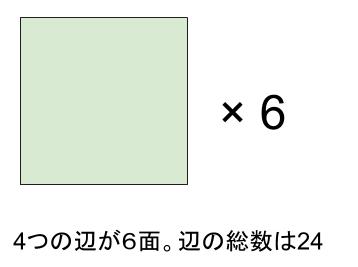
立体を、面を組みあわせてつくることを考えます。
\(6\) つの正方形がすべてバラバラのとき、辺の総数は \(4×6=24\) です。
正六面体(立方体)に組んだとき、バラバラだった辺がどうなったか見てみましょう。
必ず、\(2\) つの辺が \(1\) つになっています。
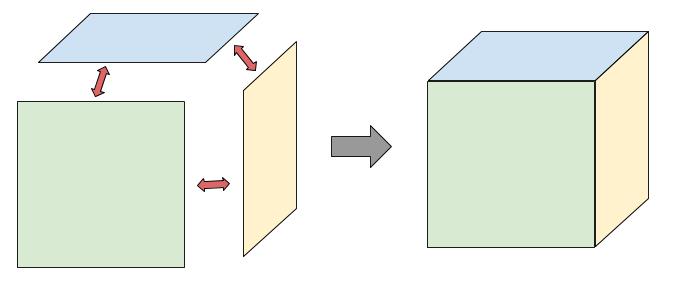
つまり、立体として組み上がると、辺の数は、バラバラだったときの半分になります。
より、正六面体(立方体)の辺の数は、\(24÷2=12\) と求まります。
この、「立体として組み上がると、辺の数は、バラバラだったときの半分」は、
あらゆる多面体で成り立ちます。
順に他の正多面体で確認しておきましょう。
正四面体
正三角形が \(4\) 面なので、バラバラのときの辺の数は、
\(3×4=12\)
立体にすると半分になるので、\(12÷2=6\)
よって、辺の数は \(6\)
正八面体
正三角形が \(8\) 面なので、バラバラのときの辺の数は、
\(3×8=24\)
立体にすると半分になるので、\(24÷2=12\)
よって、辺の数は \(12\)
正十二面体
正五角形が \(12\) 面なので、バラバラのときの辺の数は、
\(5×12=60\)
立体にすると半分になるので、\(60÷2=30\)
よって、辺の数は \(30\)
正二十面体
正三角形が \(20\) 面なので、バラバラのときの辺の数は、
\(3×20=60\)
立体にすると半分になるので、\(60÷2=30\)
よって、辺の数は \(30\)
正多面体の頂点の数の導出
オイラーの多面体定理さえ覚えておけば、正多面体の頂点の数の導出は学習しなくともなんとかなりますが・・・
辺の数の導出とほぼ同じ考え方なので、これもまとめて学習してしまいましょう。
例 正四面体
正三角形が \(4\) 面なので、バラバラのときの頂点の数は、
\(3×4=12\)
立体にすると、\(1\) つの頂点に、\(3\) つの頂点が集まっているので、\(12÷3=4\)
よって、頂点の数は \(4\)
「\(1\) つの頂点に、\(3\) つの頂点が集まっている」は、すべての多面体に共通ではありません。
各多面体ごとに異なります。
よって、各多面体の正確な見取り図がわからないと、この計算をすることはできません。
ですので、
・オイラーの多面体定理
・正 \(N\) 面体の辺の数の導出
の \(2\) つを覚えましょう。
頂点の数は、この \(2\) つから簡単に導くことができます。
スポンサーリンク
