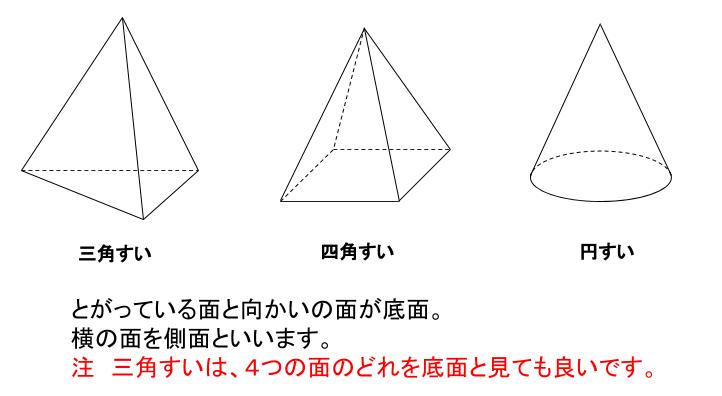
すい体の導入
とがっている立体を総称して「すい体」といいます。
上の説明はあまりにも曖昧で幼稚な言葉ですが、雰囲気をつかんでもらえればそれで問題はありません。
底面が円なら円すい、底面が四角形なら四角すい・・・柱体の名称と似ていますね。
ちなみに数学的に厳密にすい体を定義すると、非常に堅苦しく難しい言葉になります。
すい体とは、平面上の多角形または円のような閉曲線のすべての点と,平面外の一点 を結んでできた立体。
うーん、難しいですね。
あまり深入りしないでOKですよ。
とんがりの位置
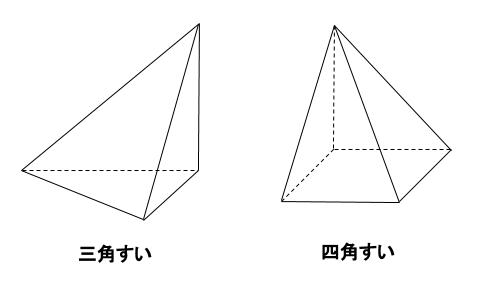
とがっている点の位置は、
下図のようにどこでもかまいません。
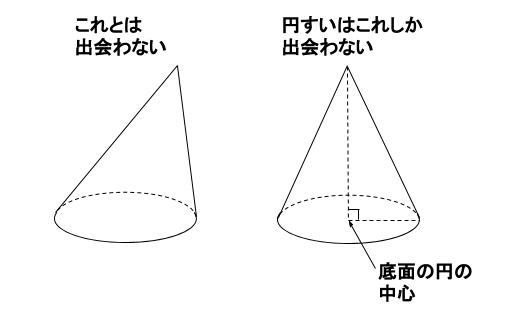
ただし、円すいのとんがりの位置は、
底面の円の中心の真上です。
これがずれている円すいを目にすることはありません。
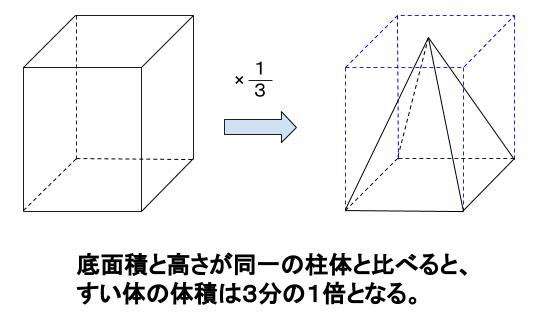
すい体の体積
\(すい体の体積=底面積×高さ×\displaystyle \frac{1}{3}\)
これは、柱体を削って、すい体を作ったならば、削る前と比較して、体積が \(\displaystyle \frac{1}{3}\) 倍になることを意味しています。
これは底面がどんな形のときにも成立します。不思議ですね!
例1
下の四角すいの体積を求めましょう。
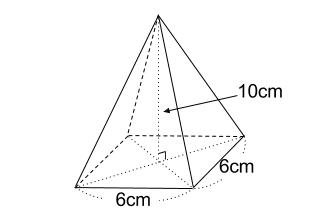
底面積は
\(6×6=36(cm^2)\)
高さは \(10cm\) なので
求める体積は
\(36×10×\displaystyle \frac{1}{3}=120(cm^3)\)
となります。
もちろん
\(6×6×10×\displaystyle \frac{1}{3}=120(cm^3)\)
と一気に計算してOKです。
例2
下の三角すいの体積を求めましょう。
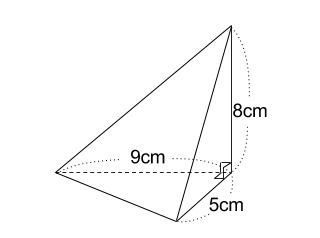
どの面を底面としても良いのですが、
\(9cm\) と \(5cm\) の \(2\) 辺をもつ面を底面としましょう。
底面積は
\(9×5×\displaystyle \frac{1}{2}(cm^2)\)
高さは \(8cm\) なので
求める体積は
\(9×5×\displaystyle \frac{1}{2}×8×\displaystyle \frac{1}{3}=60(cm^3)\)
となります。
すい体の表面積
\(すい体の表面積=底面積+側面積\)
柱体の展開図のときのように、側面積を一括してまとめることはできません。
展開図をかいて、地道に \(1\) つ \(1\) つ計算をしていきましょう。
例1
下の正四角すいの表面積を求めましょう。
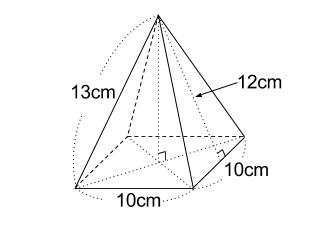
正四角すいとは、
底面が正方形の四角すいです。
展開図の一例は下の図のようになります。
底面の正方形 \(1\) つと
側面の三角形が \(4\) つ。
\(4\) つはすべて合同です。
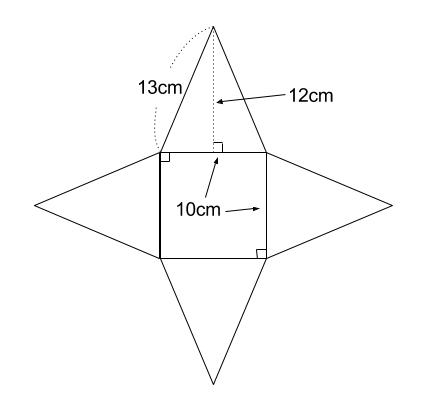
求める表面積は
底面積が \(10^2=100(cm^2)\)
側面積は三角形 \(4\) つ分で
\(10×12×\displaystyle \frac{1}{2}×4=240(cm^2)\)
よって、
\(100+240=340(cm^2)\)
となります。
\(13cm\) はまったく使わない情報でしたね。
円すいの展開図はどうなるのでしょうか。側面積は?
これについては次のページにて詳しく解説します。!
スポンサーリンク
