例題4
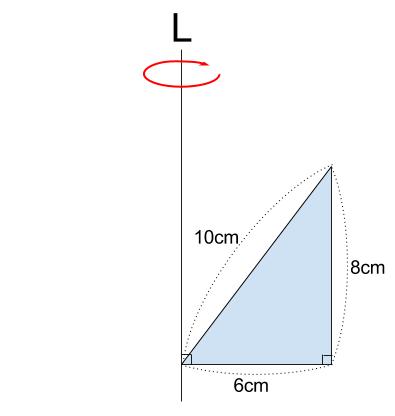
下の直角三角形を、直線 \(L\) を軸として \(1\) 回転させてできる立体について
体積と表面積をそれぞれもとめなさい。
解説
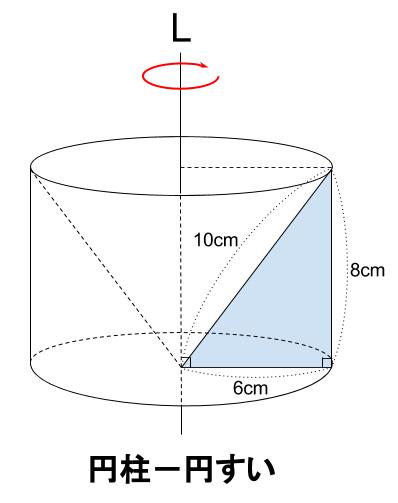
円柱から円すいをくり抜いた立体になります。
体積
体積は
\(6^2\pi×8-6^2\pi×8×\displaystyle \frac{1}{3}=192\pi\)
表面積
\(表面積=底面積+外側(円柱の側面積)\)\(+内側(円すいの側面積)\)
底面積
半径 \(6cm\) の円の面積です。
\(6^2\pi=36\pi\)
外側(円柱の側面積)
半径 \(6cm\)、高さ \(8cm\) の円柱の側面積です。
\(6×2×\pi×8=96\pi\)
内側(円すいの側面積)
半径 \(6cm\)、母線が \(10cm\) の円柱の側面積です。
\(10×6×\pi=60\pi\)
以上を合計します。
\(36\pi+96\pi+60\pi=192\pi\)
例題5
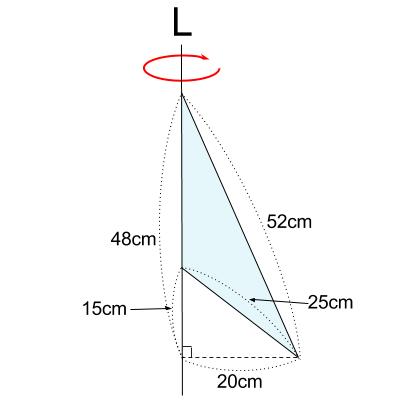
下の三角形を、直線 \(L\) を軸として \(1\) 回転させてできる立体について
体積と表面積をそれぞれもとめなさい。
解説
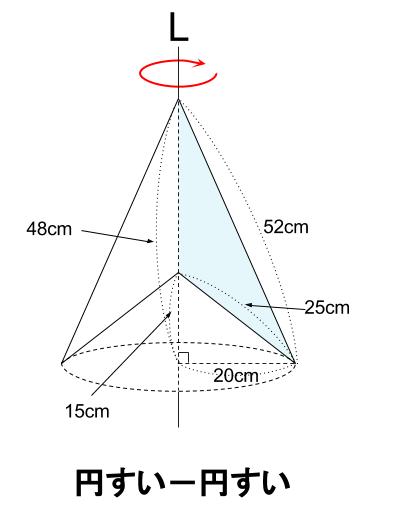
円すいから円すいをくり抜いた立体になります。
体積
\(大円すい-小円すい=体積\)
\(20^2×\pi×48×\displaystyle \frac{1}{3}-20^2×\pi×15×\displaystyle \frac{1}{3}\)
\(=20^2×\pi×(48-15)×\displaystyle \frac{1}{3}\)
\(=4400\pi\)
表面積
\(大円すいの側面+小円すいの側面=表面積\)
\(52×20×\pi+25×20×\pi\)
\(=(52+25)×20×\pi\)
\(=1540\pi\)
例題6
下の直角三角形を、直線 \(L\) を軸として \(1\) 回転させてできる立体について
体積と表面積をそれぞれ求めなさい。
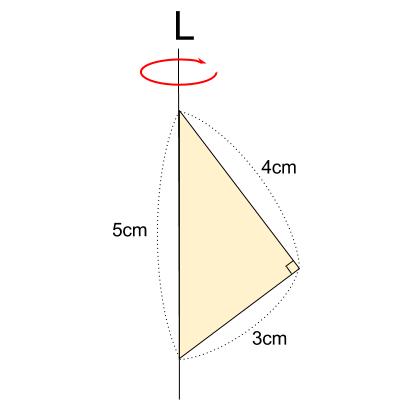
解説
\(2\) つの円すいを上下に組みあわせた立体になります。
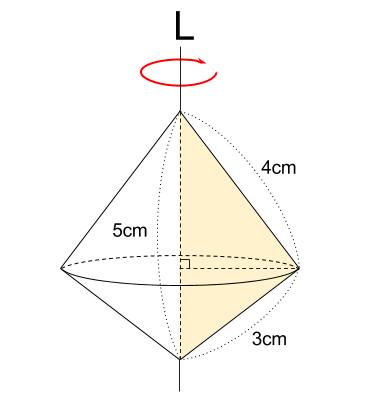
このままでは、体積も表面積も求めることはできません。
必要な長さを求めていきましょう。
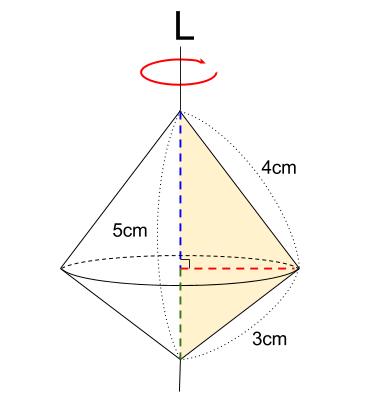
赤、青、緑の長さが求まれば、円すいの体積、表面積を求められます。
赤い長さ
赤い長さは、クリーム色の直角三角形(回転させる直角三角形)の面積から
求めることができます。
面積は、\(3×4×\displaystyle \frac{1}{2}=6\)
また、この直角三角形は、底辺を \(5cm\)、高さを赤い長さとしても面積を
求められるので、赤い長さを \(xcm\) とすれば、
\(5×x×\displaystyle \frac{1}{2}=6\)
これを解いて、
\(x=2.4\)
赤い長さが求まったので、この立体の表面積を求めることができます。
表面積
\(上の円すいの側面積+下の円すいの側面積=表面積\)
\(4×2.4×\pi+3×2.4×\pi\)
\(=(4+3)×2.4×\pi\)
\(=16.8\pi\)
体積
青い長さが上の円すいの高さ、
緑の長さが下の円すいの高さ、
これらが求まらないと体積は計算できなそうですが、
実は、ここは省略できます。
青い長さを \(ycm\)、
緑の長さを \(zcm\)
として、体積の計算をします。
\(上の円すいの体積+下の円すいの体積=体積\)
\(2.4^2×\pi×y×\displaystyle \frac{1}{3}+2.4^2×\pi×z×\displaystyle \frac{1}{3}\)
\(=2.4^2×\pi×(y+z)×\displaystyle \frac{1}{3}\)
ここで、\(y+z=5\) を代入します。
また、\(2.4= \displaystyle \frac{12}{5}\) とおきかえます。
分数は約分ができるため、小数よりも計算が楽になることが多いのです。
よって、
\((\displaystyle \frac{12}{5})^2×\pi×5×\displaystyle \frac{1}{3}\)
\(=\displaystyle \frac{48}{5}\pi\)
参考 \(y\) 、\(z\) も求めることができます
中学3年生になると、「相似(そうじ)」という図形の考え方を学習します。
これを用いると、\(y=3.2cm\) 、\(z=1.8cm\) と求めることができます。
スポンサーリンク
