回転なので、当然ですが、円に関わる立体が出来上がります
円柱、円すい、それらを組み合わせた立体になります。
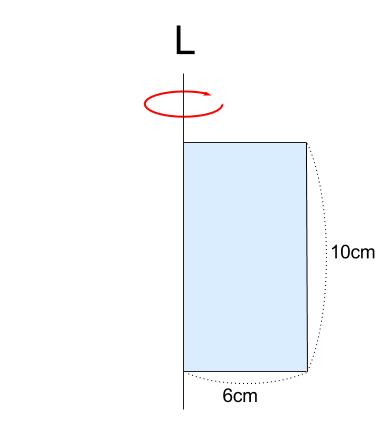
例題1
下の長方形を、直線 \(L\) を軸として \(1\) 回転させてできる立体について
体積と表面積をそれぞれもとめなさい。
解説
円柱になります。
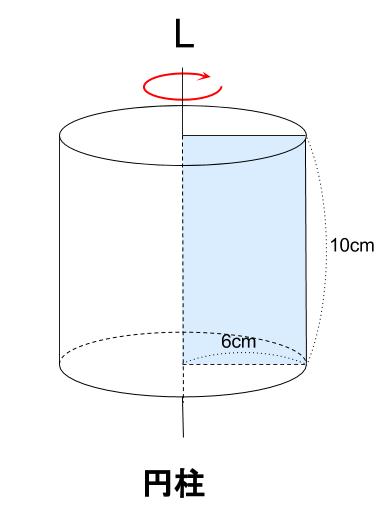
体積
\(体積=底面積×高さ\)
\(6^2\pi×10=360\pi\)
表面積
\(表面積=底面積×2+側面積\)
\(6^2\pi×2+6×2×\pi×10\)
\(=72\pi+120\pi\)
\(=192\pi\)
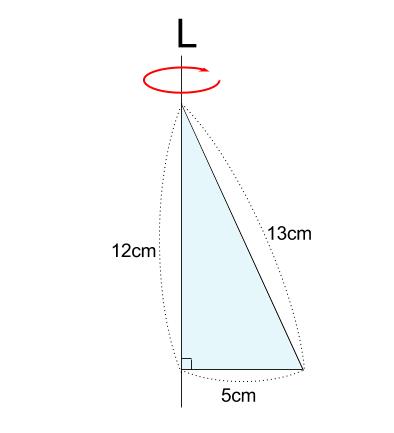
例題2
下の直角三角形を、直線 \(L\) を軸として \(1\) 回転させてできる立体について
体積と表面積をそれぞれもとめなさい。
解説
円すいになります。
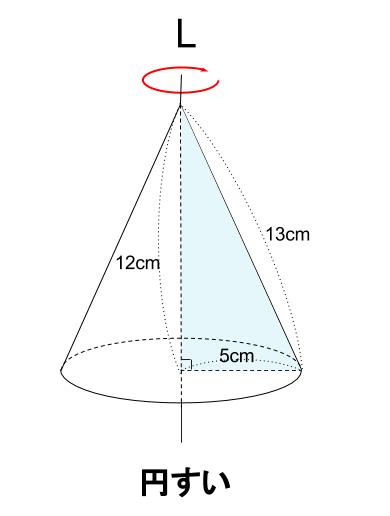
体積
\(体積=底面積×高さ× \displaystyle \frac{1}{3}\)
\(5^2\pi×12×\displaystyle \frac{1}{3}=100\pi\)
表面積
\(表面積=底面積+側面積\)
\(5^2\pi+13×5×\pi\)
\(=25\pi+65\pi\)
\(=90\pi\)
例題3
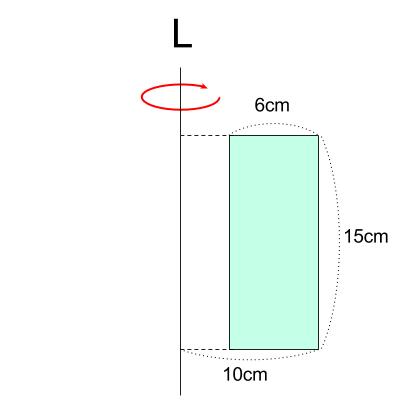
下の長方形を、直線 \(L\) を軸として \(1\) 回転させてできる立体について
体積と表面積をそれぞれもとめなさい。
解説
トイレットペーパーのような立体になります。
円柱から、円柱をくりぬいた立体です。
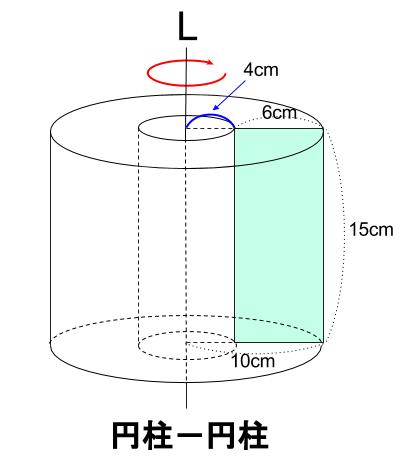
体積
\(体積=底面積×高さ\)
底面積は、ドーナツのような図形の面積です。
大円から小円を引けば良いですね。
つまり、
\((10^2\pi-4^2\pi)×15=1260\pi\)
表面積
\(表面積=底面積 2つ +側面 2つ\)
底面積
底面積はドーナツにような形が上下に \(2\)つです。
\((10^2\pi-4^2\pi)×2=168\pi\)
側面積
側面積は外側と内側がありますね。
外側の側面積
半径 \(10cm\) の円柱の側面積になります。
\(10×2×\pi×15=300\pi\)
内側の側面積
半径 \(4cm\) の円柱の側面積になります。
\(4×2×\pi×15=120\pi\)
いよいよ表面積!
以上を合計します。
\(168\pi+300\pi+120\pi=588\pi\)
これが求める答えとなります。
スポンサーリンク
